(a,b)–Bäume
Binäre Suchbäume erreichen für insert, delete und locate meistens logarithmische Zeit. Im schlimmsten Fall können alle Operationen jedoch lineare Zeit brauchen, das passiert, wenn der Baum keine logarithmische, sondern lineare Tiefe hat. Da in jeder der drei Operationen ein Pfad durch den Baum traversiert wird, erhalten wir die lineare Laufzeit. Wir wollen allerdings immer logarithmischer Laufzeit. Das erreichen wir, durch Bäume die immer balanciert sind – ein Beispiel dafür sind (a, b)-Bäume. Diese haben stets logarithmische Höhe und Laufzeit.
Binärbaume können zu hoch wachsen
Wenn wir eine Liste erhalten, und aus dieser einen binären Suchbaum konstruieren, so kann es passieren, dass wir eine lange Kette von Knoten produzieren. Wollen wir nun, beispielsweise, einen Schlüssel suchen, müssen wir die gesamte Kette entlang laufen. Das Problem besteht also darin, dass der Baum lineare Tiefe hat, und wir den längsten Pfad traversieren müssen.
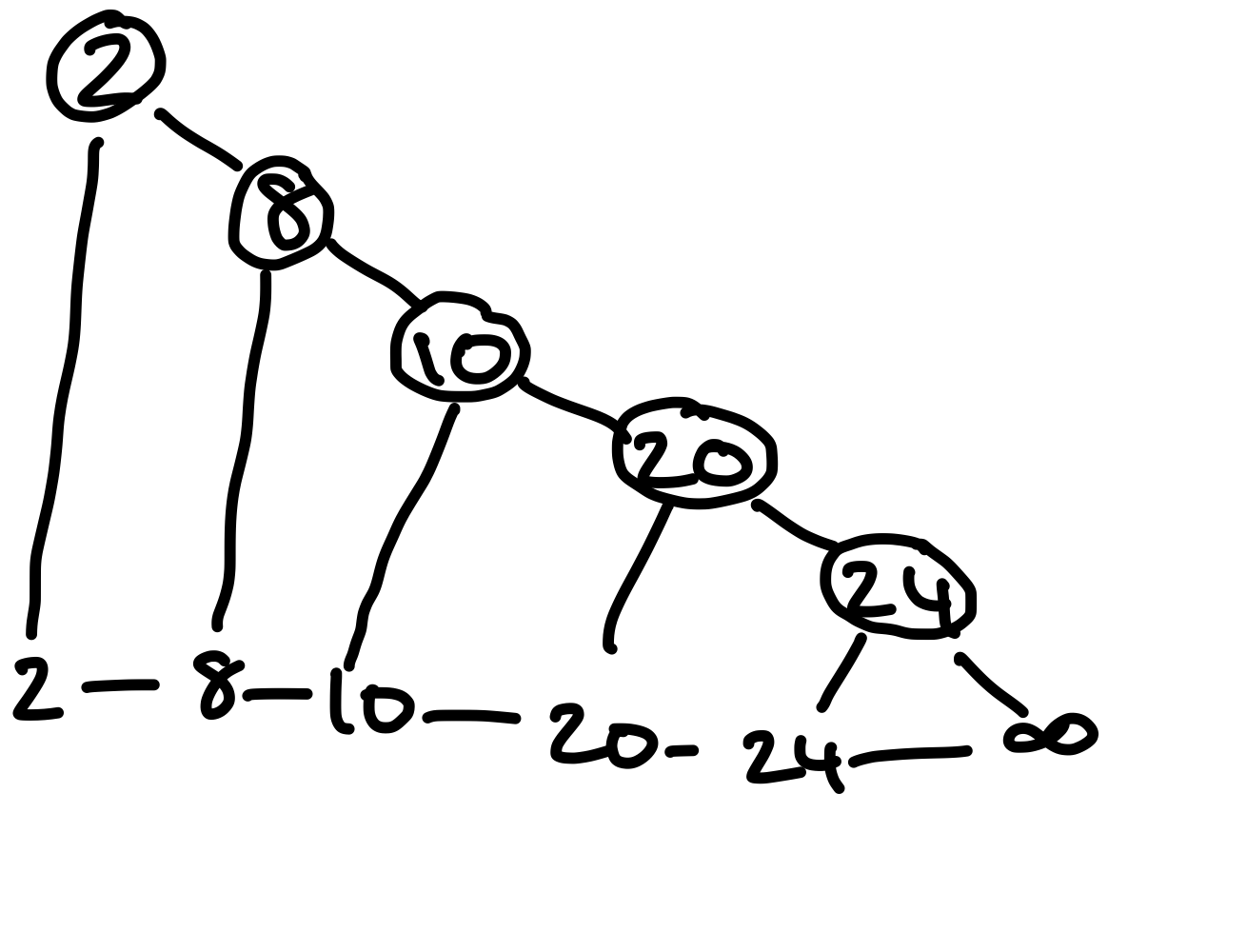
Figure 1: Ein degenerierter, binärer Suchbaum. Er hat lineare Tiefe. Dieser entsteht durch sukzessives einfügen der Elemente 2, 8, 10, 20, 24.
Betrachten wir den gegebenen binären Suchbaum, um das Problem zu veranschaulichen. Wir suchen nach dem Schlüssel \(k=24\). Zuerst vergleichen wir \(k\) mit der Wurzel, und sehen, dass \(2 \leq k\), weshalb wir zum rechten Kind gehen. Anschließend müssen wir erneut zum rechten Kind gehen. Das wiederholt sich für alle verbleibenden Knoten, bis wir am Blatt angekommen sind. Dann haben wir unseren Schlüssel gefunden.
Interessanterweise können wir dieselben Schlüssel in einem binären Suchbaum logarithmischer Tiefe anordnen. Allgemein existiert für jede Folge von Schlüsseln ein binärer Suchbaum logarithmischer Tiefe – allerdings können wir nicht garantieren, dass wir diesen immer konstruieren, da seine Form von der Reihenfolge abhängt, in der wir Schlüssel einfügen. Dieselben Schlüssel, lediglich in anderer Reihenfolge, produzieren den folgenden binären Suchbaum – mit logarithmische Tiefe!
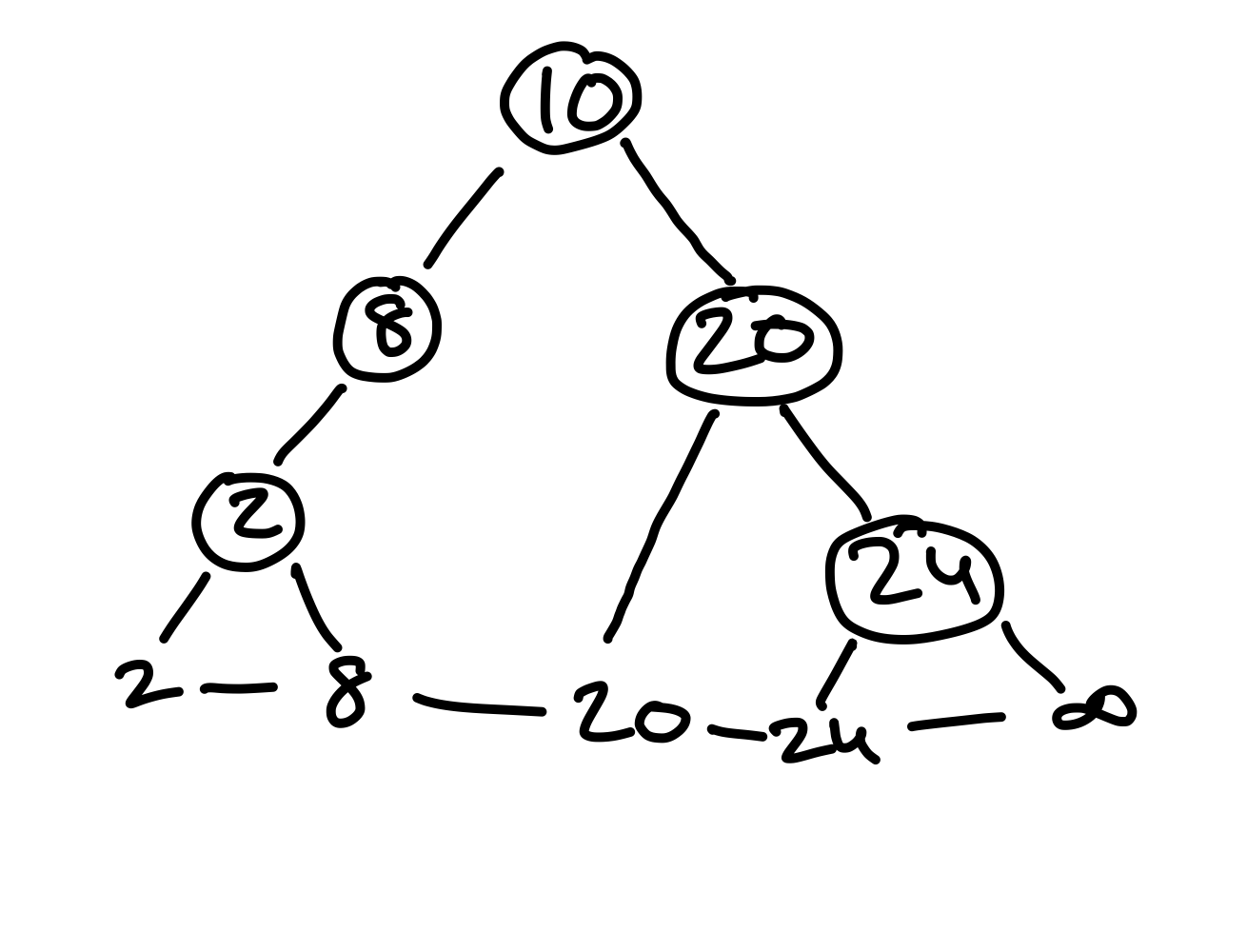
Figure 2: Dieser binäre Suchbaum enthält dieselben Elemente, wie der vorherige. Hier wurden sie lediglich in der Reihenfolge 10, 8, 20, 2, 24, eingefügt.
Mindestens 2, maximal 4 Kinder
Selbst wenn wir statt zwei Kindern drei erlauben würden, entstehen immernoch degenerierte Bäume. Tatsächlich produziert die Folge aus dieser Abbildung immer denselben Baum, egal wieviele Kinder wir maximal erlauben. Ein Perspektivwechsel liefert den zündenden Gedanken: wenn jeder Knoten mehr als ein Kind haben muss, entstehen solche Bäume nicht.
So erhalten wir die erste Eigenschaft von (a, b)-Bäumen: alle Knoten haben mindestens \(a\) und maximal \(b\) viele Kinder. Konkret hat jeder Knoten in einem (2, 4)-Bäume zwischen zwei und vier Kinder. Der folgende Baum entspricht dieser Anforderung.
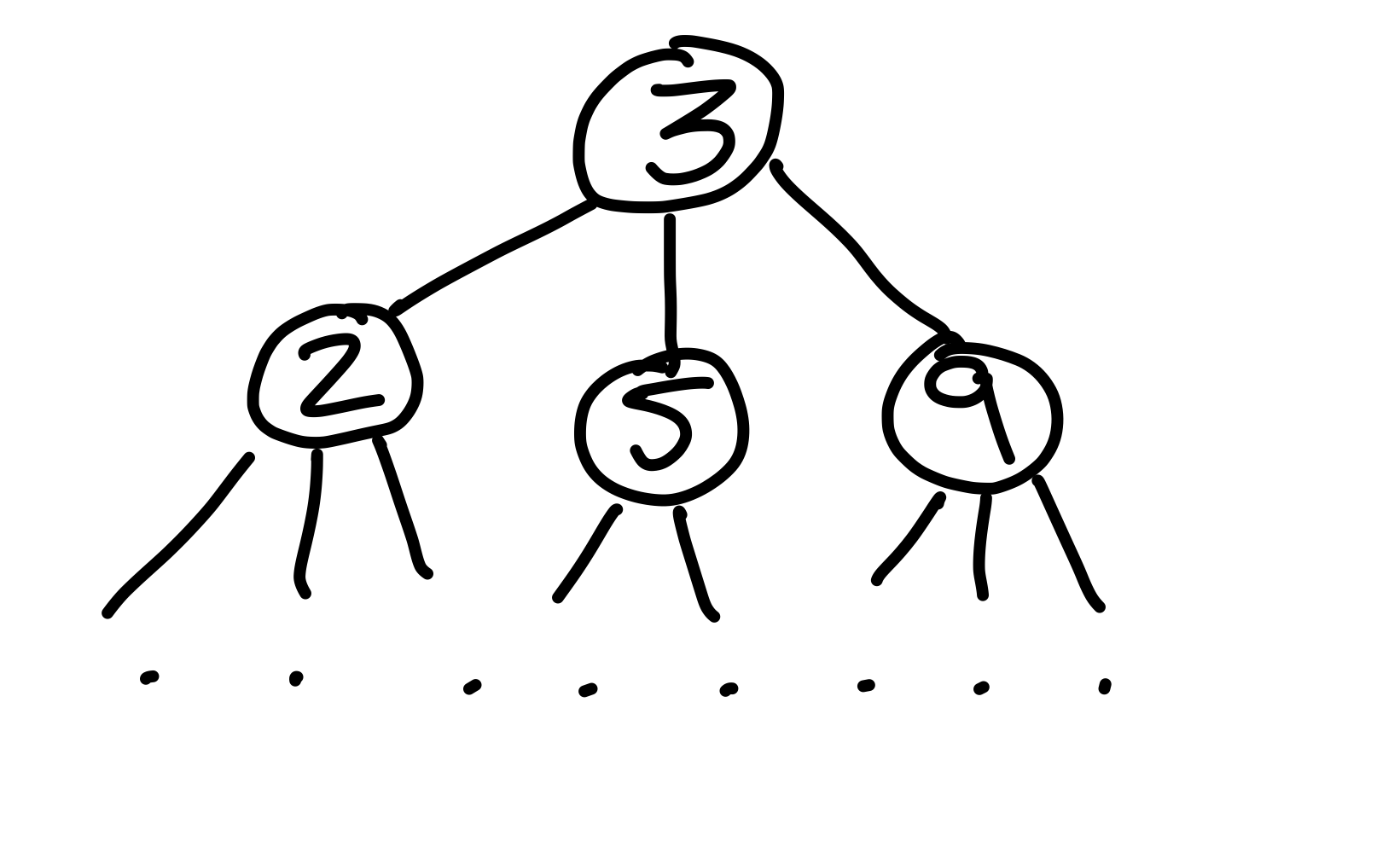
Figure 3: So könnte ein (2, 4)-Baum, von der Form, aussehen. Im Vergleich zu Binärbaumen haben manche Knoten mehr als zwei Kinder.
Das sieht erstmal gut aus, allerdings haben wir nun ein subtiles Problem. Angenommen ich möchte in diesem Baum nun nach dem Schlüssel \(k=5\) suchen, dann vergleiche ich zuerst \(k\) mit der Wurzel, in diesem Fall ist \(k \geq 3\), weshalb wir das linke Kind nicht besuchen müssen – dieses enthalt schließlich alle Schlüssel die kleiner gleich \(3\) sind. Welches der verbleibenden Kinder is das Richtige? Du kannst die Frage beantworten, indem Du den Baum genauer betrachtest, jedoch müssen wir unseren Computer befähigen das zu tun. Mit der Information, die wir aus der Wurzel haben, ist das nicht möglich. Wir müssen mehr Informationen in den Knoten speichern.
Genauso, wie die \(3\) uns zeigt, dass alle Schlüssel im linken Teilbaum kleiner gleich drei sind, können wir die \(8\) speichern, welche größer gleich allen Schlüsseln in dem mittleren Teilbaum ist. Vergleiche ich jetzt \(k=5\) mit der Wurzel, so vergleiche ich zusätzlich mit der \(8\). Jetzt kann ich entscheiden, zu welchem Kind ich gehe: ist \(k \leq 3\), dann gehe ich links. Ist \(3 \leq k \leq 8\), dann gehe ich zum mittleren Kind. Andernfalls muss \(k > 8\) sein, weshalb ich zum rechten Teilbaum gehe. Wir haben unser Problem gelöst, indem wir mehr Elemente in dem Knoten speichern, diese geben uns jeweils Schranken für die Werte der Teilbäume.
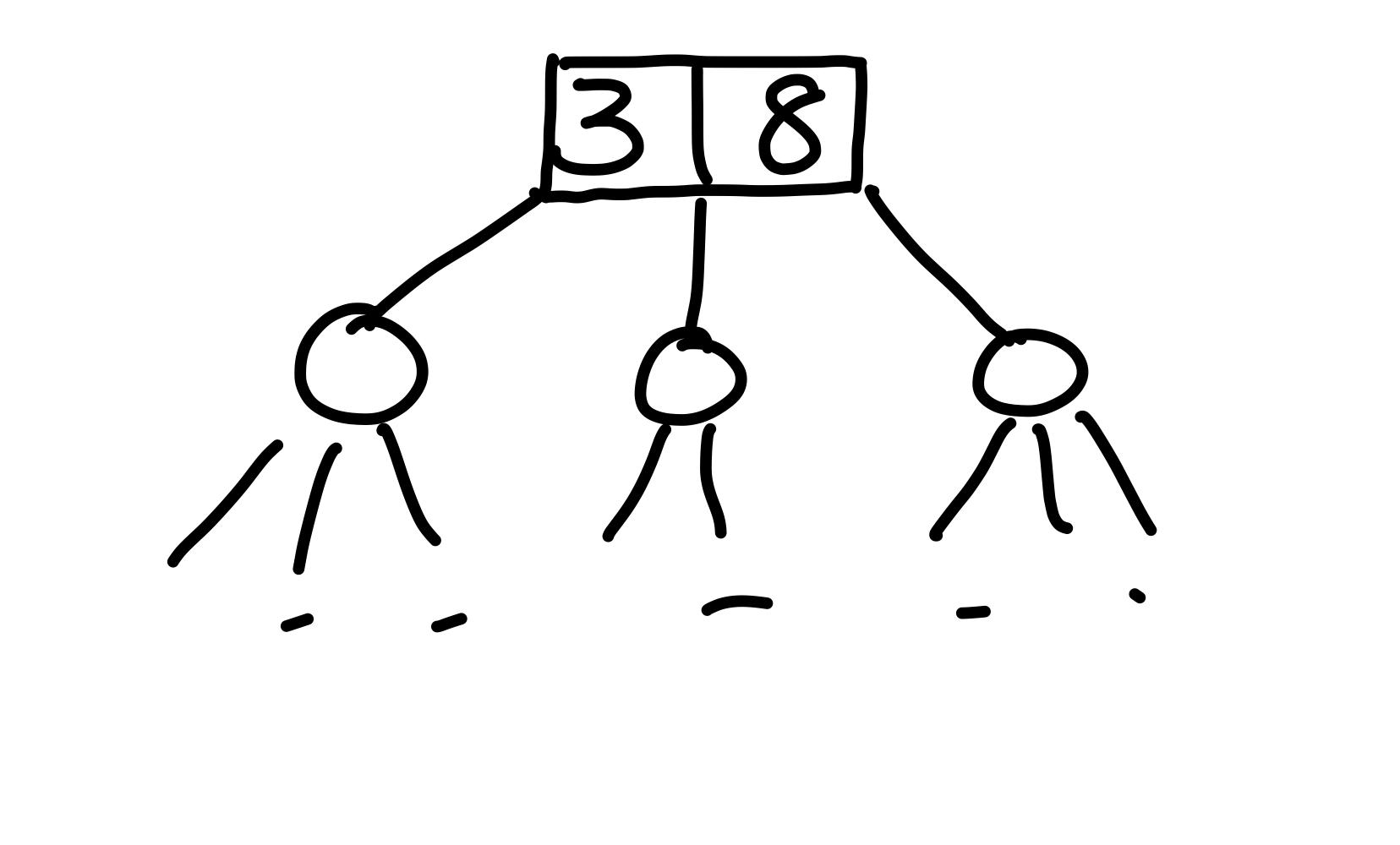
Figure 4: Die Wurzel speichert nun zwei, statt einem Schlüssel. So können wir bei einer Suche wissen, zu welchem Kind wir gehen müssen.
Locate
Zuvor haben wir informell gesehen, wie man in einem (2, 4)-Baum nach einem Schlüssel sucht. Nun betrachten wir den konkreten Algorithmus.
Locate geht bei Eingabe \(k\) wie folgt vor:
- Vergleiche \(k\) mit den Elementen im aktuellen Knoten, um zum korrekten Kind zu gehen.
- Wiederhole Schritt eins solange, bis Du an einem Blatt angekommen bist.
- Entspricht das Blatt dem Schlüssel, so können wir diesen zurückgeben. Wenn nicht, so gehen wir über die verkettete Liste der Blätter zum nächstgrößeren Eintrag, und geben diesen zurück.
Schritt eins und zwei entsprechen dem, was wir zuvor an einem Beispiel getan haben. Allerdings kann der dritte Schritt erstmal unintuitiv wirken; warum ist es hilfreich, das nächstgrößere Element zu erhalten, wenn wir nach einem bestimmten \(k\) gefragt haben? Dafür müssen wir die Situationen betrachten, in denen (a, b)-Bäume genutzt werden. Ein häufiges Anwendungsgebiet sind Datenbanken. So stellen Nutzer Bereichsanfragen, um alle Werte zu erhalten, die in einer bestimmten Reichweite liegen. Für einen online shop könnte man alle Einkaufe im Juli erfragen. Was aber, wenn es am 1. Juli keinen Einkauf gab? Dann wäre der nächstgrößere Eintrag gesucht – solange dieser noch im Juli liegt.
Wenden wir die Schritte aus locate einmal auf einen etwas höheren (2, 4)-Baum an, welcher in dem Bild hierunter gegeben ist. Dafür suchen wir nun nach dem Schlüssel \(k=41\).
- Zuerst vergleichen wir \(k\) mit der Wurzel. Da \(k > 17\), gehen wir zum rechten Kind.
- Hier ist \(25 \leq k \leq 41\). Daher gehen wir zum Kind zwischen \(25\) und \(41\).
- Nun gilt \(k > 30\), wir gehen also zum rechten Teilbaum.
- Wir sind an einem Blatt angekommen, das den gesuchten Schlüssel hat. Wir geben diesen als Ergebnis aus.
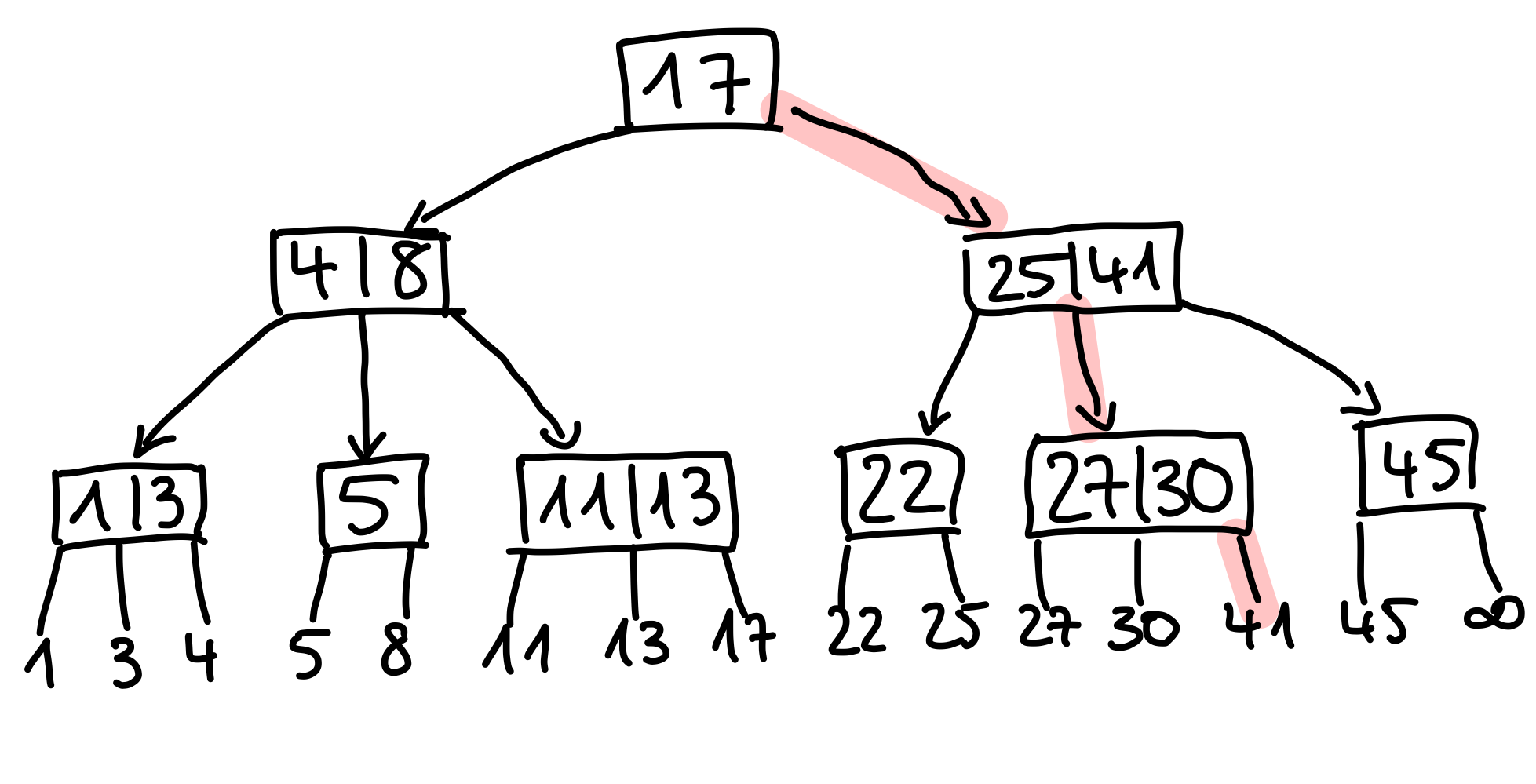
Figure 5: Der Weg von locate ist rot markiert.
Ein solides Verständnis des locate Algorithmus ist wichtig, da ihn alle weiteren Operationen nutzen. Egal, ob wir einen Schlüssel löschen, oder hinzufügen wollen, wir müssen zuerst eine geeignete Stelle in der Liste finden – durch locate.
Wir bauen einen Baum
Bis jetzt haben wir auf bereits konstruierten (a, b)-Bäumen gesucht; wie wir sie konstruieren wissen wir aber nicht. Häufig erhalten wir eine Liste mit Elementen, und sollen aus dieser einen initialen (a, b)-Baum erstellen. Das tun wir, indem wir die Elemente der Liste nacheinander in einen anfangs leeren Baum einfügen. Wenn wir das probieren, werden wir mit drei Problemen konfrontiert:
- Die Wurzel kann zu Beginn die (a, b)-Bedingung verletzen.
- Wir wollen nicht nur in die Liste, sondern auch in den Baum einfügen, weshalb wir den eingefügten Wert in dem passenden Knoten speichern müssen.
- Beim hinzufügen zu einem Knoten kann es passieren, dass dieser zu viele Kinder hat. Wir müssen die Kinder irgendwie aufteilen.
Es sei die Liste \(L = \langle 2, 7, 12, 4, 8, 3, 5, 6, 9 \rangle\) gegeben. Wir konstruieren im Folgenden, schrittweise, einen (3, 5)-Baum, um das erste Problem genauer zu betrachten.
Einen (a, b)-Baum konstruieren wir, durch sukzessives Einfügen, ähnlich den binären Suchbäumen. Das bedeutet, der neue Schlüssel \(k\) muss sowohl in der veketteten Liste, als auch in der Baumstruktur, an der korrekten Stelle eingefügt werden. Glücklicherweise liefert locate eine passende Position in der verketteten Liste, und löst ein weiteres Problem: Wenn das einzufügende Element in der Liste existiert, sagt locate uns das. In diesem Fall muss nichts eingefügt werden.
Wenn wir das erste Element einfügen wollen, so müssen wir es in einen leeren (a, b)-Baum einfügen. Der muss erstmal definiert werden. Außerdem: wie soll ich in einen Baum einfügen, der nicht existiert? Schließlich kann ich kein Element locaten. Dafür machen wir uns das Leben leichter, indem der leere Baum nicht wirklich leer ist. Stattdessen enthält er einen Dummy-Knoten, welcher keinem tatsächlichem Wert entspricht, uns aber erlaubt Elemente zu locaten. Somit sieht der leere Baum, der manchmal auch der triviale Baum genannt wird, so aus.

Figure 6: Der triviale Baum enthält nur den Dummy-Knoten.
Interessanterweise verletzt der triviale Baum die (3, 5)-Bedingung – die Wurzel hat Grad eins. Das lässt sich nicht verhindern, weshalb die (a, b)-Bedingung für die Wurzel entspannt wird, sie muss einen Grad zwischen zwei und \(b\) haben. Insbesonders hat sie Grad eins nur für den trivialen Baum. So haben wir das erste Problem bereits gesehen, und gelöst. Nun können wir endlich anfangen Elemente einzufügen.
Wir fügen \(2\) ein, indem wir zuerst nach der \(2\) suchen. Die Wurzel ist leer, weshalb es der triviale Baum sein muss, weshalb wir das linke Kind, mit dem Schlüssel \(2\), erstellen und in der Liste verketten.
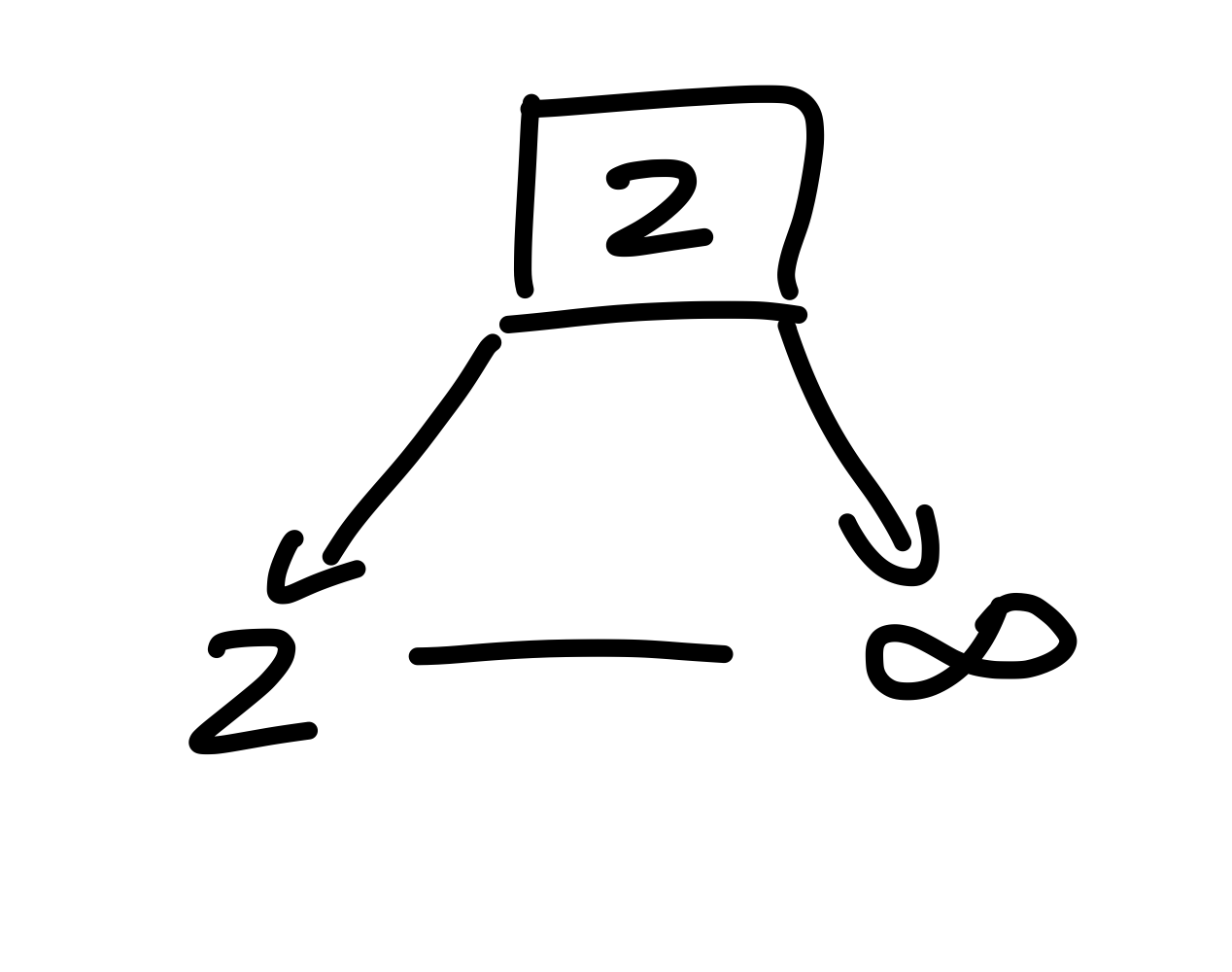
Figure 7: Nachdem wir 2 in den trivialen Baum einfügen.
Nun fällt uns aber auf, dass die \(7\) keinen Elternknoten besitzt; vielleicht könnte das zu einem Problem werden. Wir ignorieren das erstmal, und fügen weiter ein, als nächstes die \(12\). Auf der Suche landen wir bei der zwei und fügen deshalb die \(12\) nach der \(2\) in die Liste ein Jetzt sehen wir bereits das Problem: Die verkettete Liste ist nicht sortiert. Eine naive Lösung könnte sein, die \(12\) an der richtigen Stelle einzufügen, indem wir solange die verkettete Liste entlang gehen, bis wir einen geeigneten Platz gefunden haben. Dann ist die verkettete Liste zwar sortiert, wir kriegen jedoch Probleme mit der Laufzeit, da im schlimmsten Fall die gesamte Liste traversiert werden muss, weshalb wir \(\mathcal{O}(n)\) Laufzeit haben. Zusätzlich stellt sich nun die Frage, wozu wir überhaupt den (a, b)-Baum haben, wenn dieser nichts bringt.
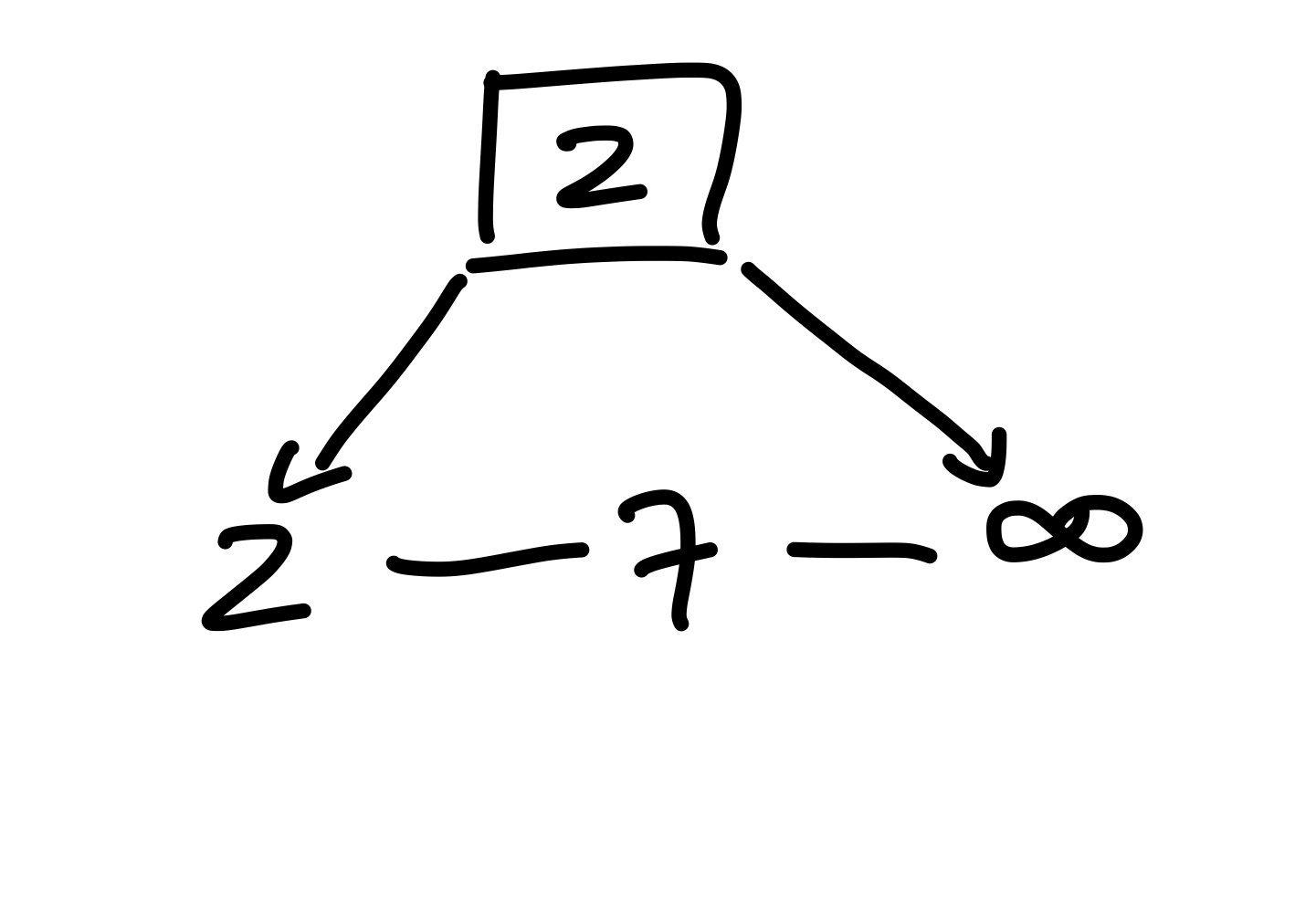
Figure 8: Die 7 wird in der Blattliste eingefügt.
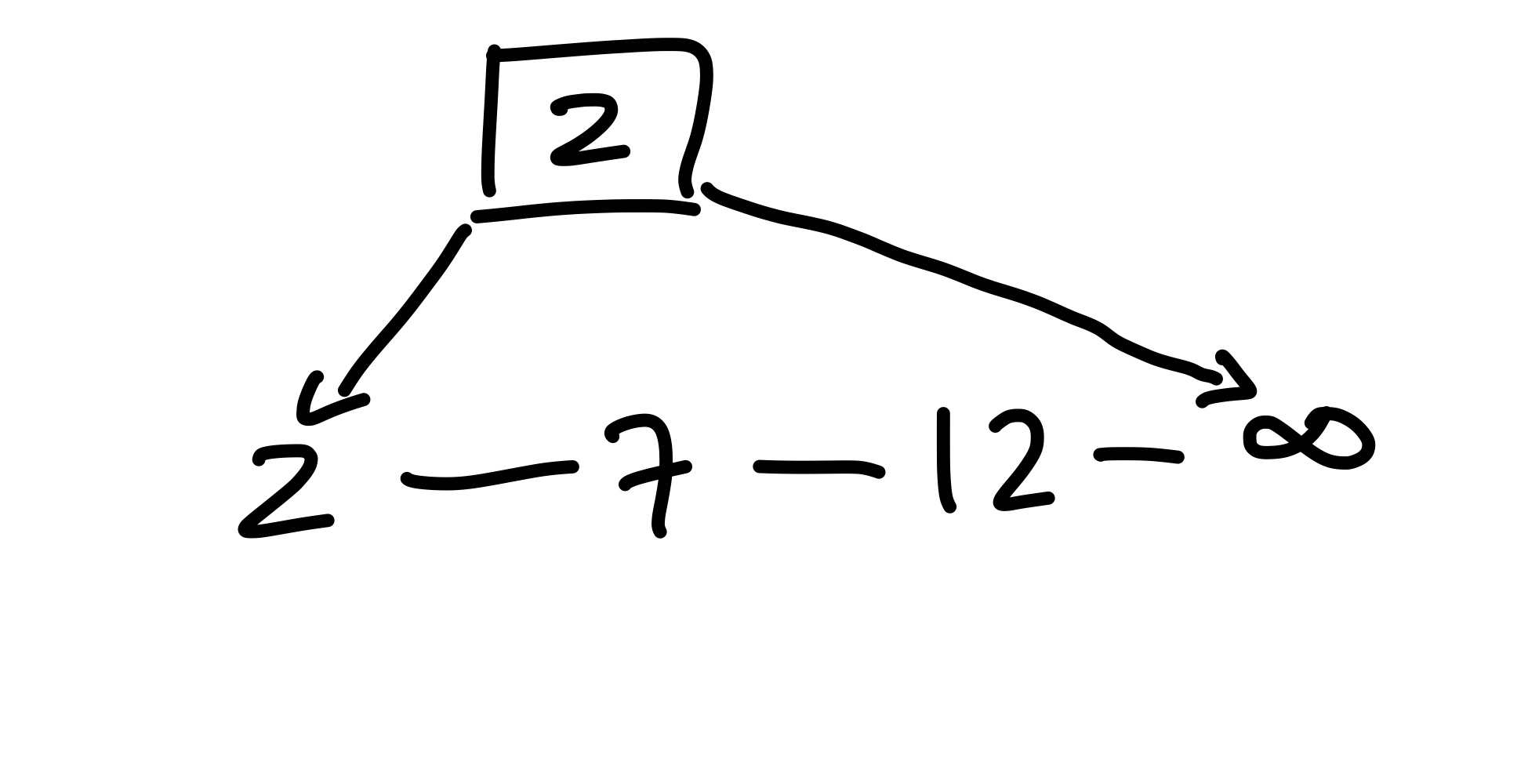
Figure 9: Die 12 wird in der Blattliste eingefügt.
Um eine logarithmische Laufzeit zu erhalten, müssen wir von der Wurzel aus direkt, über einen Pfad, zu einem potentiellen Blatt gehen. Es liegt also nahe, in der Wurzel einen Verweis zur \(7\) zu speichern, und das ist genau die Lösung. Wenn wir einen Schlüssel einfügen, müssen wir diese in die Schlüsselliste des Elternknoten einfügen. Das gilt bereits für unsere erste Einfügeoperation, die \(2\). Wir fangen nochmal mit dem trivialen Baum an, und fügen diesmal Schlüssel korrekt ein. Die \(2\) fügen wir zu Beginn der verketteten Liste ein, und speichern diese im Elternknoten. Danach fügen wir die \(7\) ein.
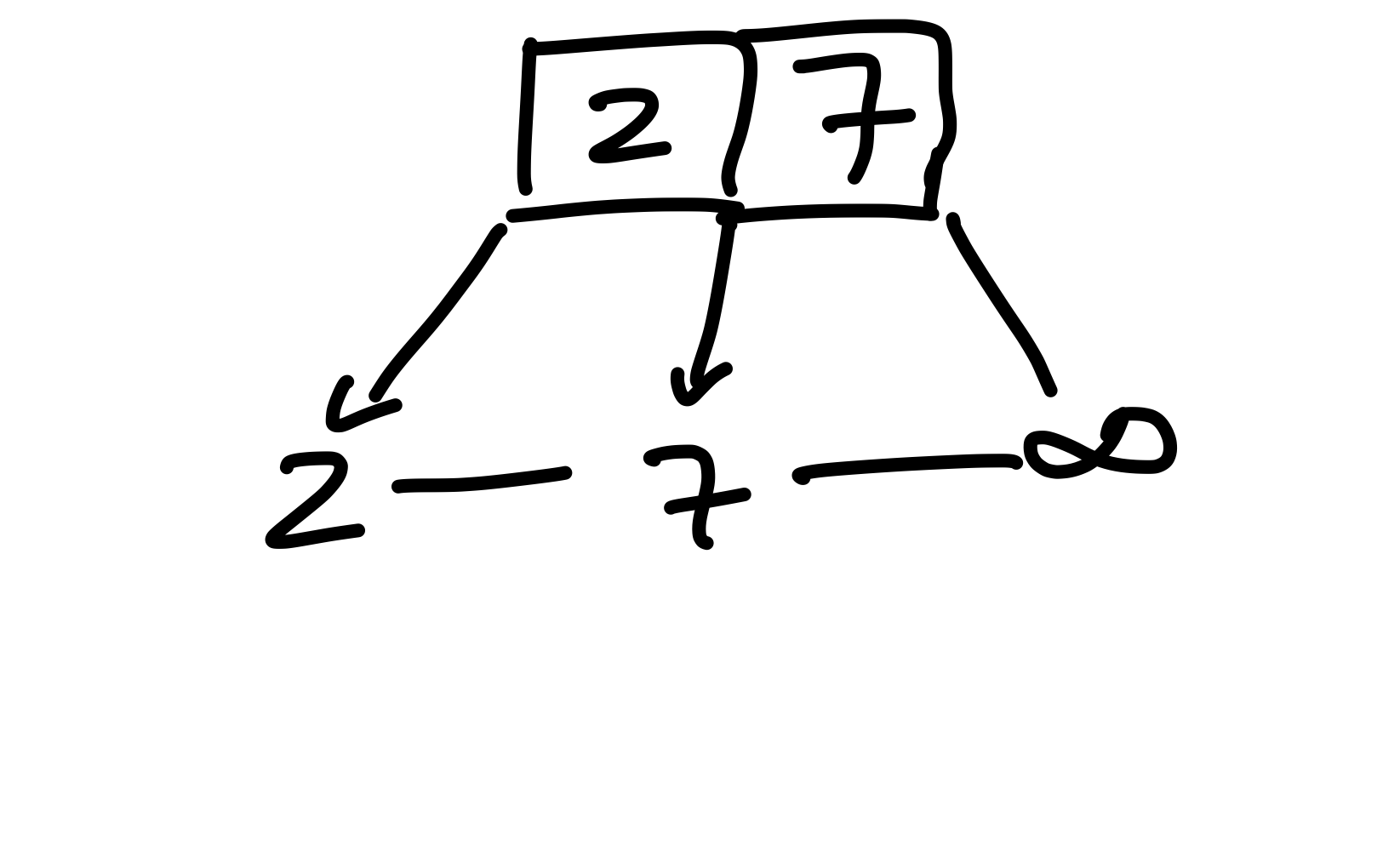
Figure 10: Hier wurden 2 und 7 in den trivialen Baum eingefügt, allerdings haben wir die Schlüssel auch in dem Elternknoten hinterlegt.
Die \(12\) einfügen ist ähnlich zur \(7\), wir landen beim Dummy-Knoten und fügen \(12\) davor ein. Auch die Schlüsselliste wird aktualisiert und wir erhalten:
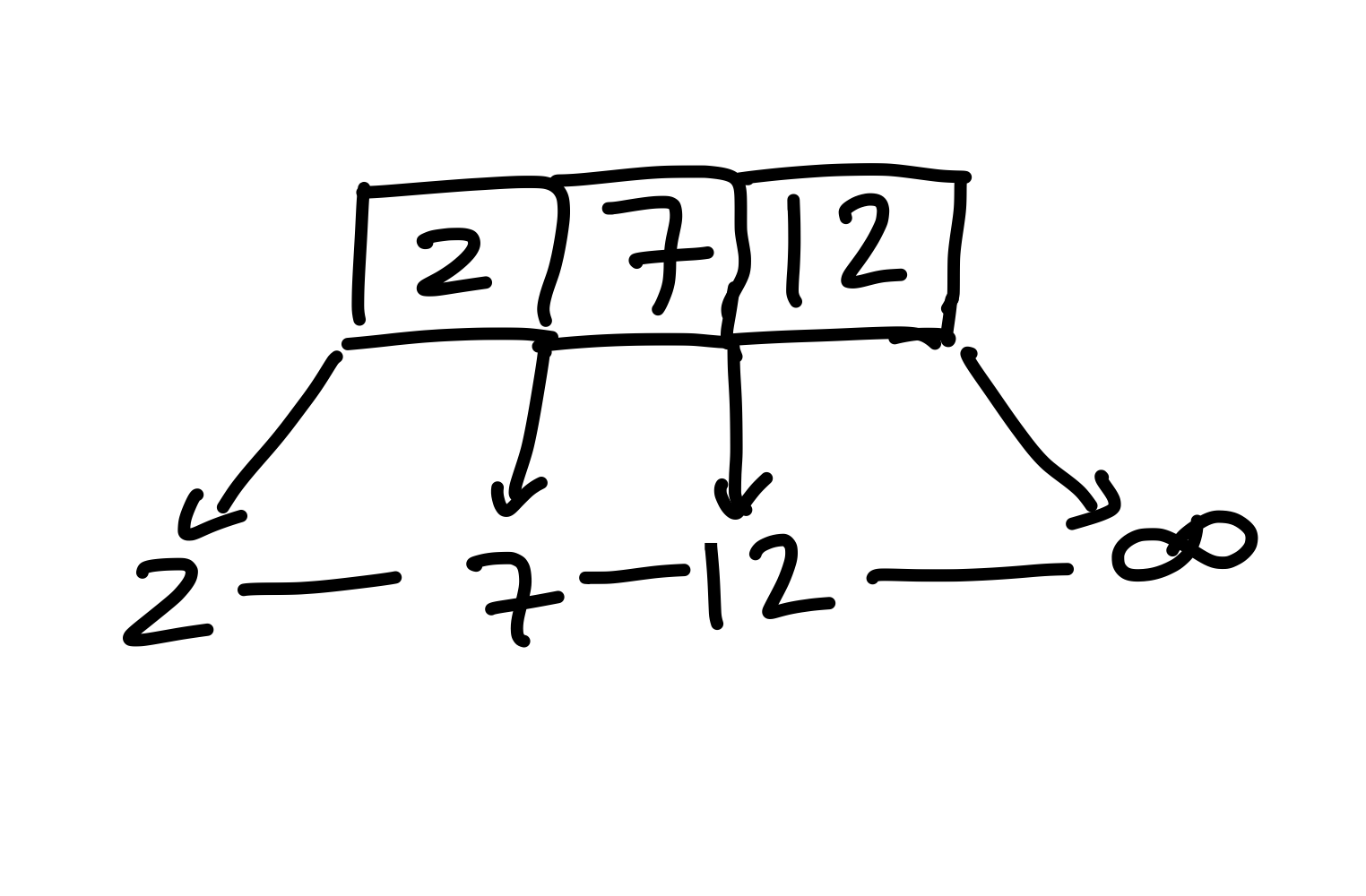
Figure 11: Wie zuvor fügen wir die (12) an der richtigen Stelle der verketteten Liste, und im Elternknoten, ein.
Wenn wir \(k=4\) einfügen, gehen wir zum Blatt mit dem Schlüssel \(7\), da \(2 \leq k \leq 7\). Dort angekommen fügen wir die \(4\) vor der \(7\) ein, und aktualisieren den Elternknoten.
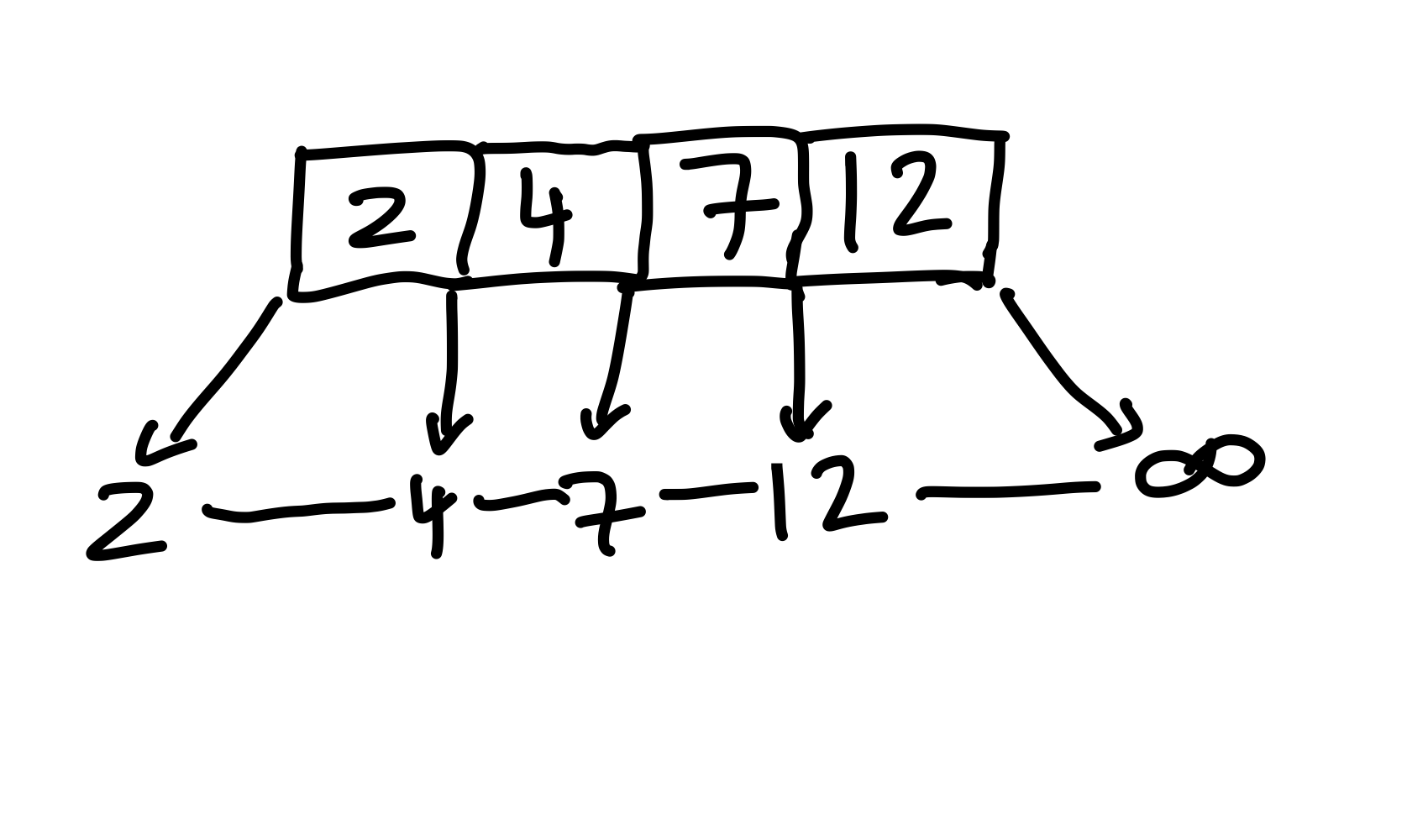
Figure 12: Nun wird die 4 eingefügt.
Bei allen vorherigen inserts erfüllt die Wurzel die (3, 5)-Bedingung. Durch den nächsten insert wird diese jedoch verletzt. Nachdem wir die \(8\) einfügen, hat unsere Wurzel \(6\) Kinder.
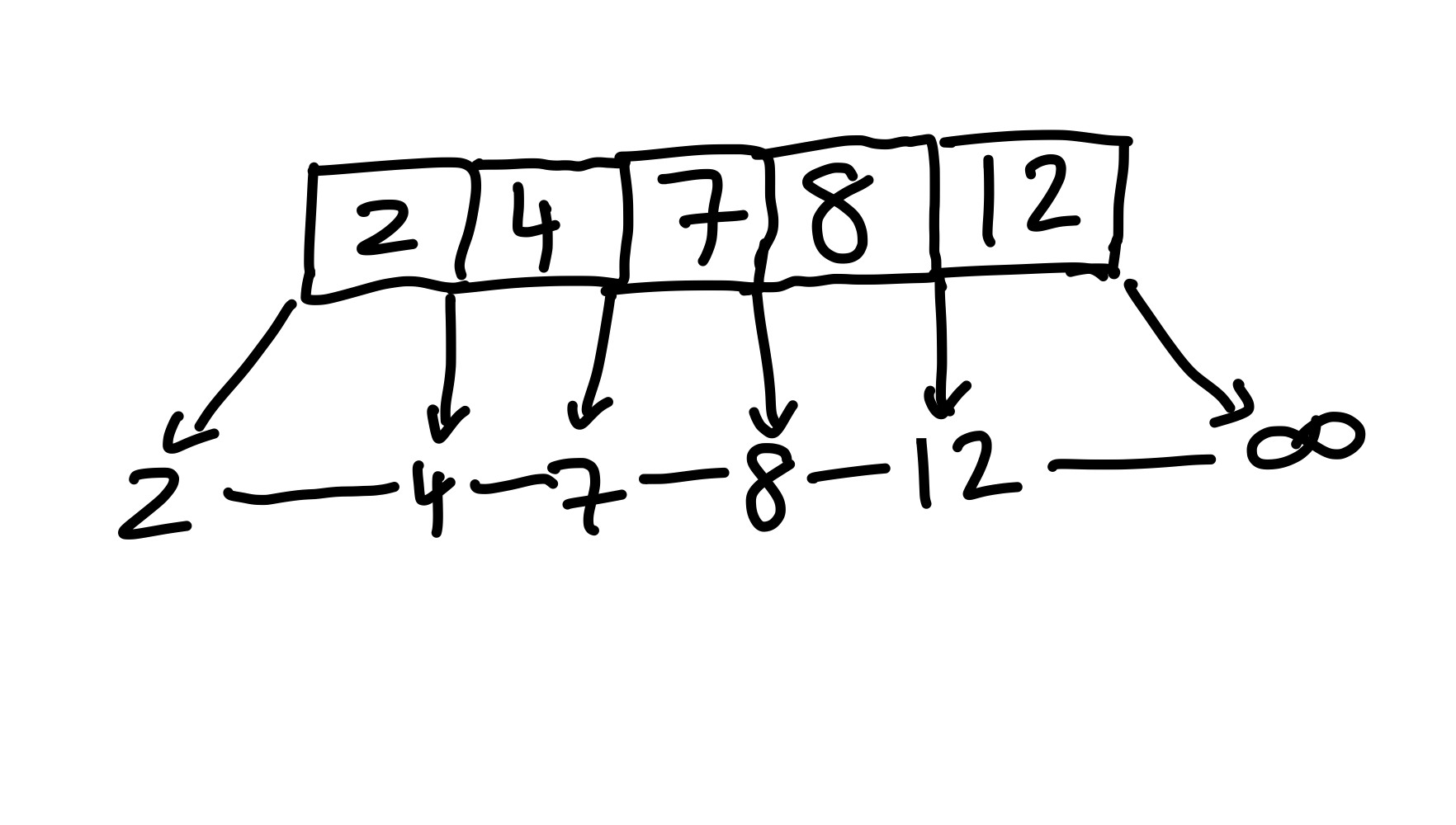
Figure 13: Nachdem wir die 8 einfügen, hat die Wurzel zu viele Kinder.
Jetzt sehen wir das dritte Problem: Ein Knoten hat zu viele Kinder. Allerdings können wir nicht einfach Kinder löschen, sonst verlieren wir diese und unser Baum wird fehlerhaft. Daher müssen wir den überfüllten Knoten in drei neue Knoten aufteilen: einen Elternknoten, einen linken und rechten Kinderknoten. Die Frage ist, wie genau wir aufteilen. Dafür bietet es sich an, den mittleren Schlüssel als neuen Elternknoten zu wählen, dann sind das linke und rechte Kind ca. gleich groß. Hier wird also die \(7\) zu einem neuen Elternknoten.
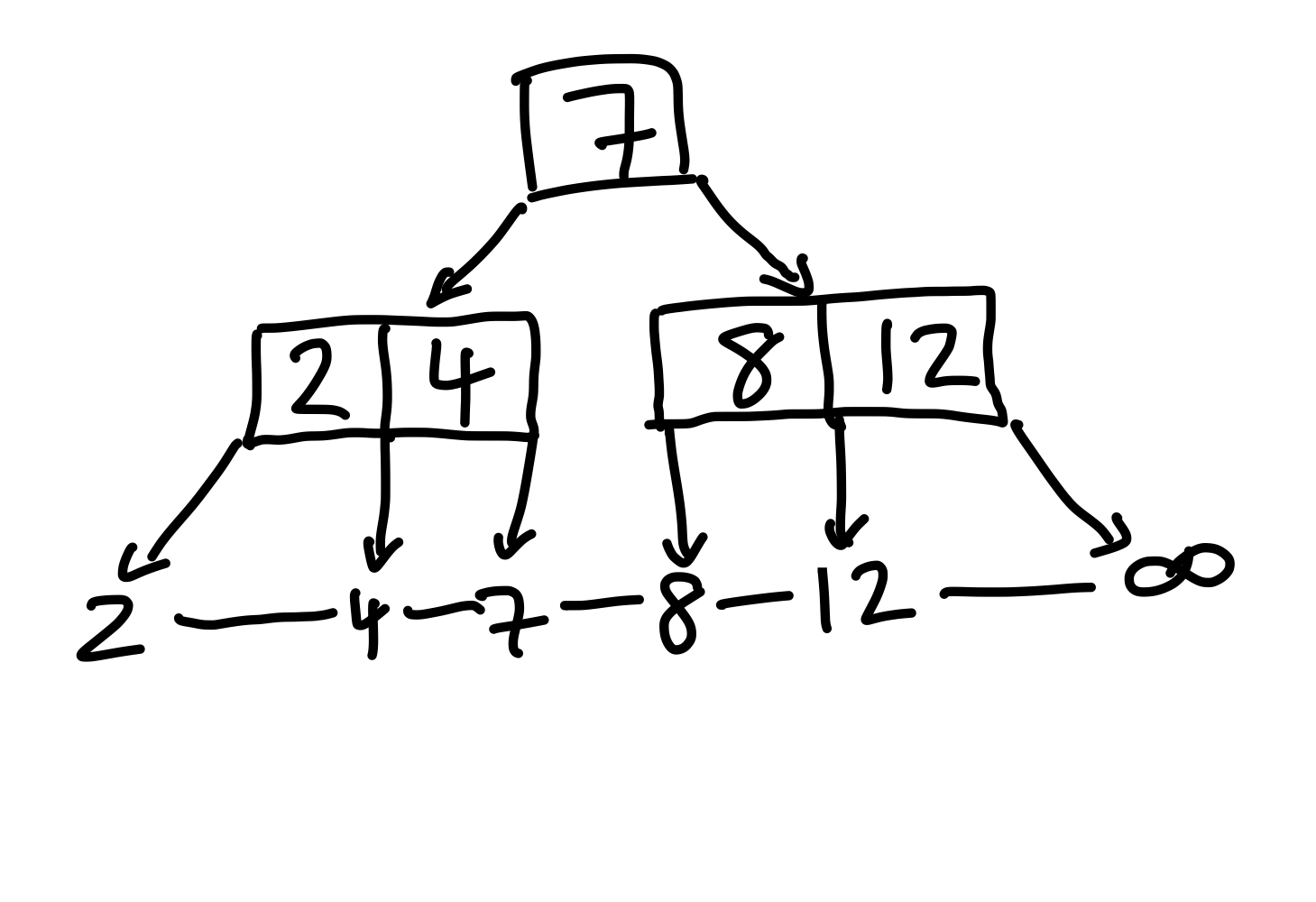
Figure 14: Der vorherige Overflow wurde gelöst, indem wir die Wurzel aufteilen.
Die \(9\) einzufügen ist einfach, da nichts besonderes passiert.
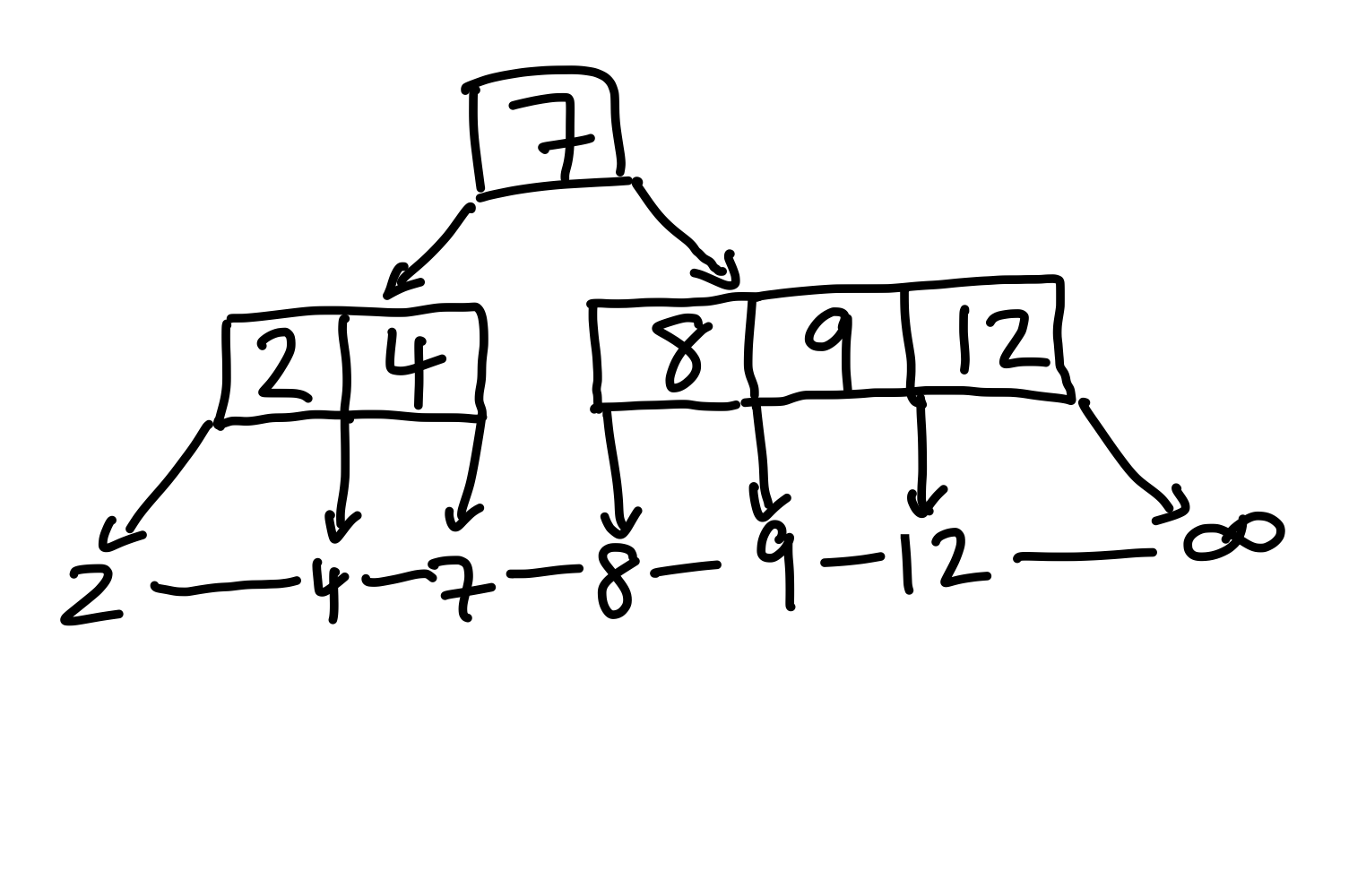
Figure 15: Nach einfügen der 9.
Nun fügen wir der Reihe nach \(3, 5\) und \(6\) in den Baum ein. Alle werden in den linken Kinderknoten eingefügt, da sie kleiner als \(7\) sind.
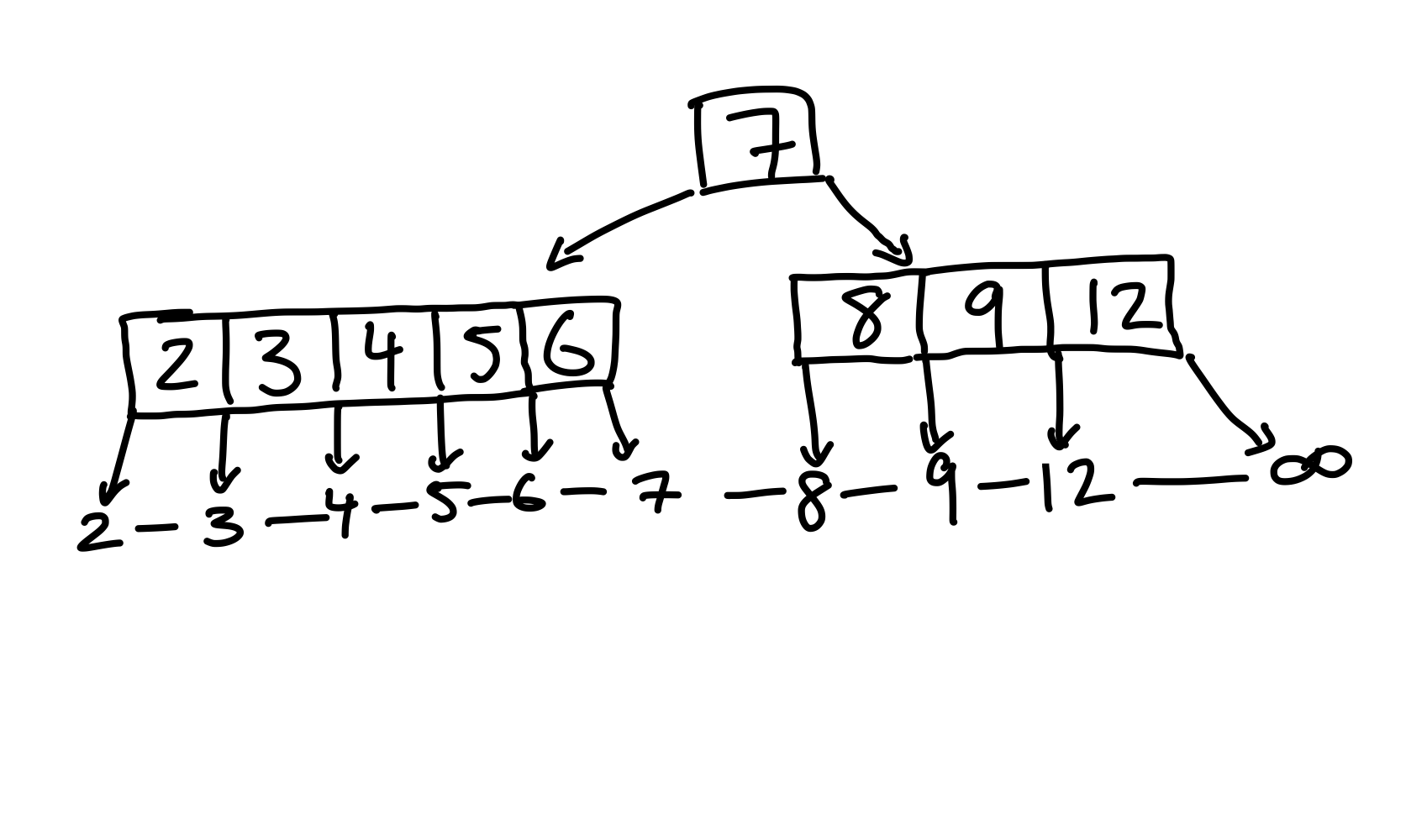
Figure 16: Das linke Kind hat zu viele Kinder. Wir müssen es aufteilen.
Jetzt ist der linke Kinderknoten zu groß, und muss aufgeteilt werden. Wie zuvor wählen wir den mittleren Schlüssel, in diesem Fall \(4\) als neuen Elternknoten. Jetzt ist aber nicht ganz klar, was mit dem neuen Elternknoten passiert. Naiv gesehen haben wir zwei Optionen, entweder wir fügen den so erhaltenen Teilbaum an die Wurzel an – das entspricht dem ersten Bild – oder, wir fügen den Elternknoten in die Wurzel ein.
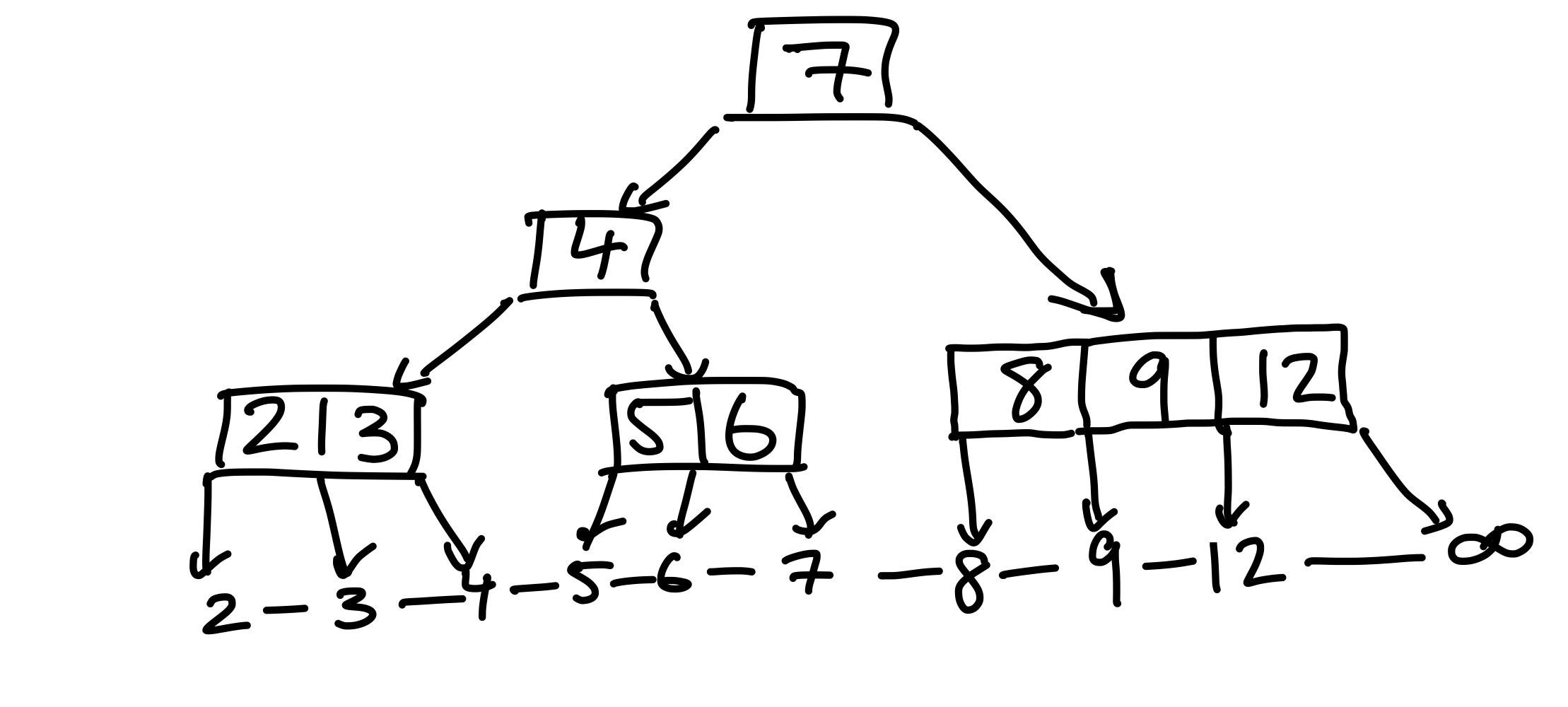
Figure 17: Eine Möglichkeit, das linke Kind aufzuteilen. Hier erhöhen wir die Höhe des gesamten Baumes um eins.
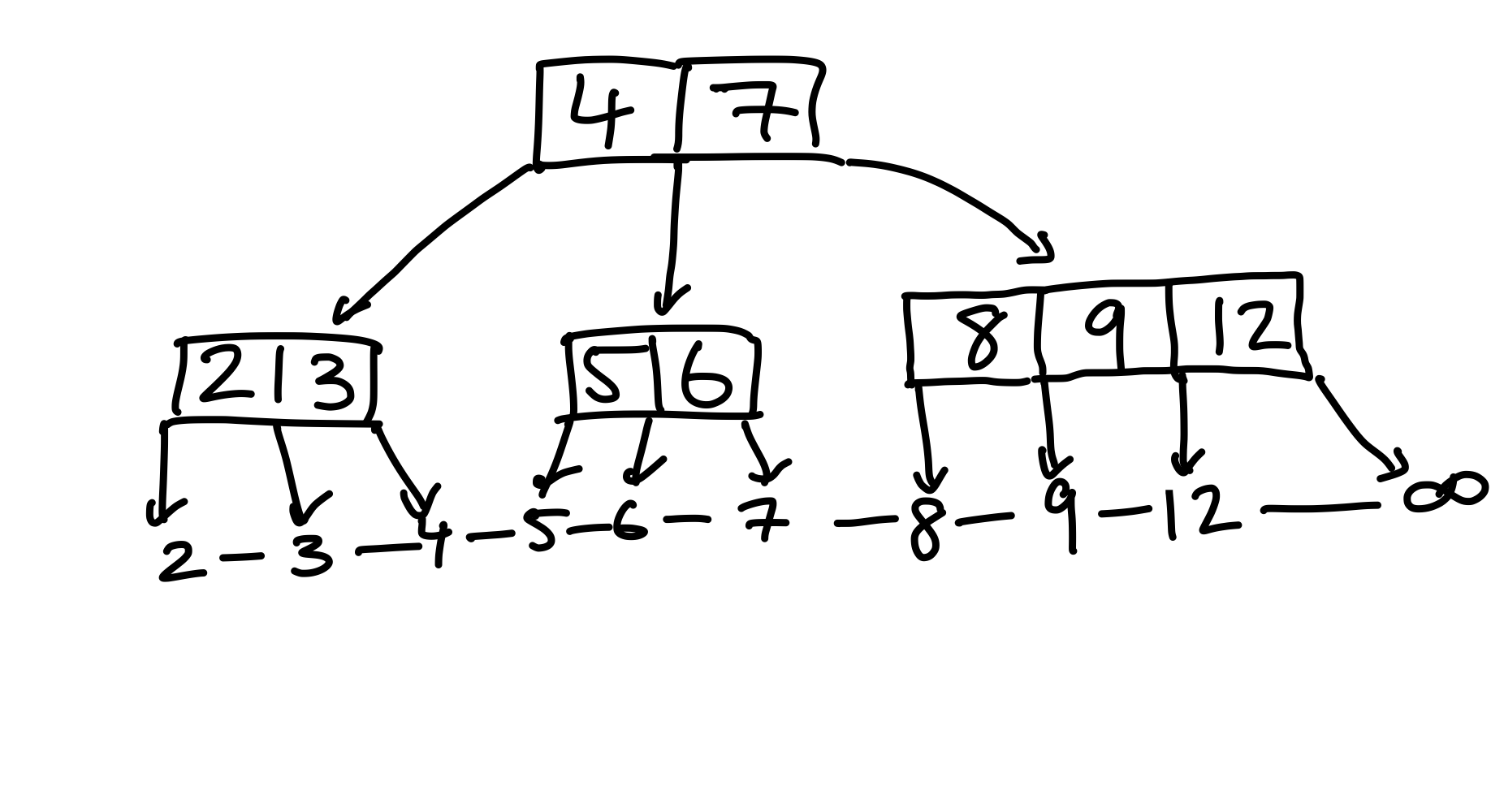
Figure 18: Hier haben wir den entstehenden Elternknoten direkt in die Wurzel gemerged.
Schlüssel löschen
Wir können: (a, b)-Bäume bauen, Schlüssel finden, und Schlüssel hinzufügen. Alles was fehlt ist, Schlüssel zu löschen. Während Knoten durch inserts zuviele Kinder haben können, haben Knoten u.U. zu wenig Kinder, wenn wir welche löschen. Sobald das passiert, müssen wir Schlüssel aus anderen Knoten hinzufügen.
Fangen wir naiv an, aus der verketteten Liste Schlüssel zu löschen. Dafür starten wir mit dem (3, 5)-Baum aus dem vorherigen Abschnitt. Löschen wir zuerst die \(6\). Wie immer fangen wir damit an, die \(6\) zu suchen, und anschließend aus der verketteten Liste zu löschen.
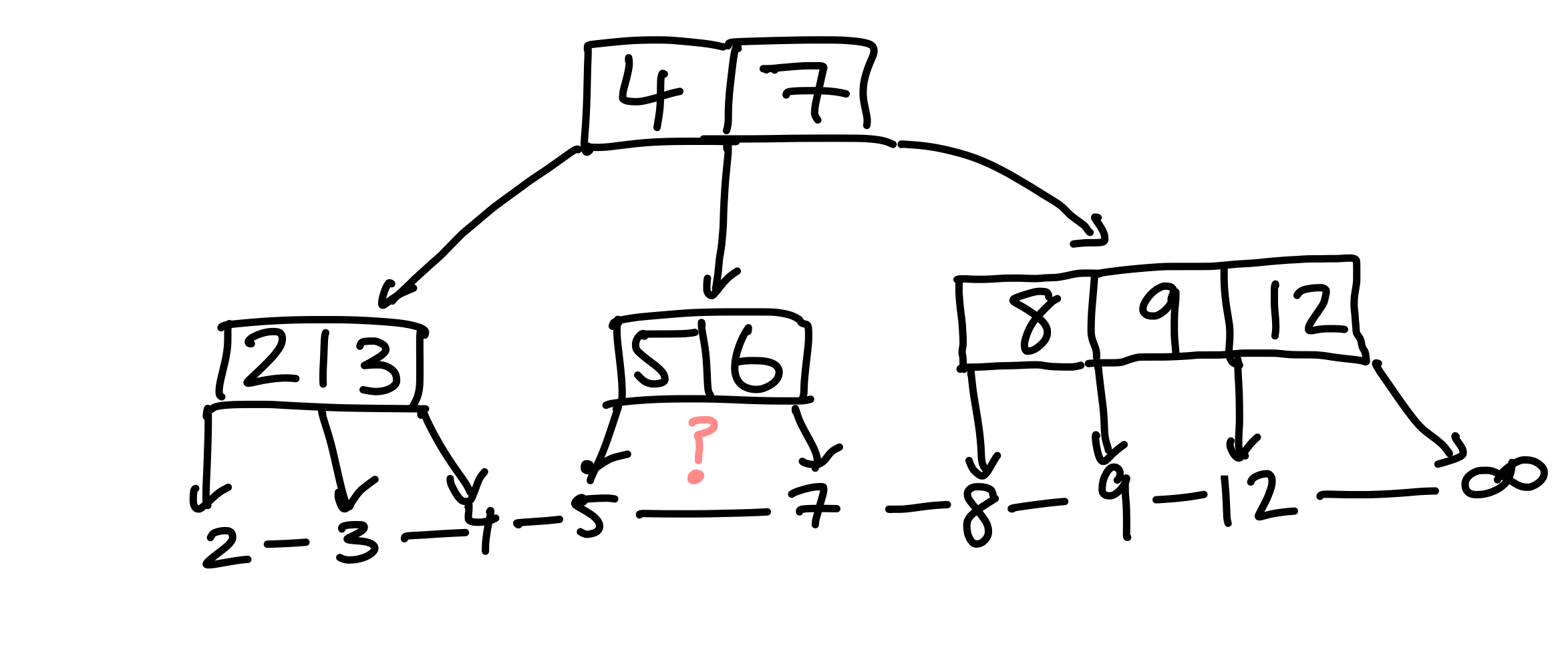
Figure 19: Nachdem wir die 6 aus der verketteten Liste löschen, fehlt ein Zeiger.
Allerdings fällt auf, dass die \(6\) immernoch in dem Elternknoten ist, obwohl es kein Blatt mit der \(6\) gibt. Falls wir nun nach der \(6\) suchen, verweist dieser Elternknoten auf ein nicht existierendes Blatt. Aus diesem Grund wollen wir bei einer remove Operation den Schlüssel zusätzlich aus dem Baum löschen.
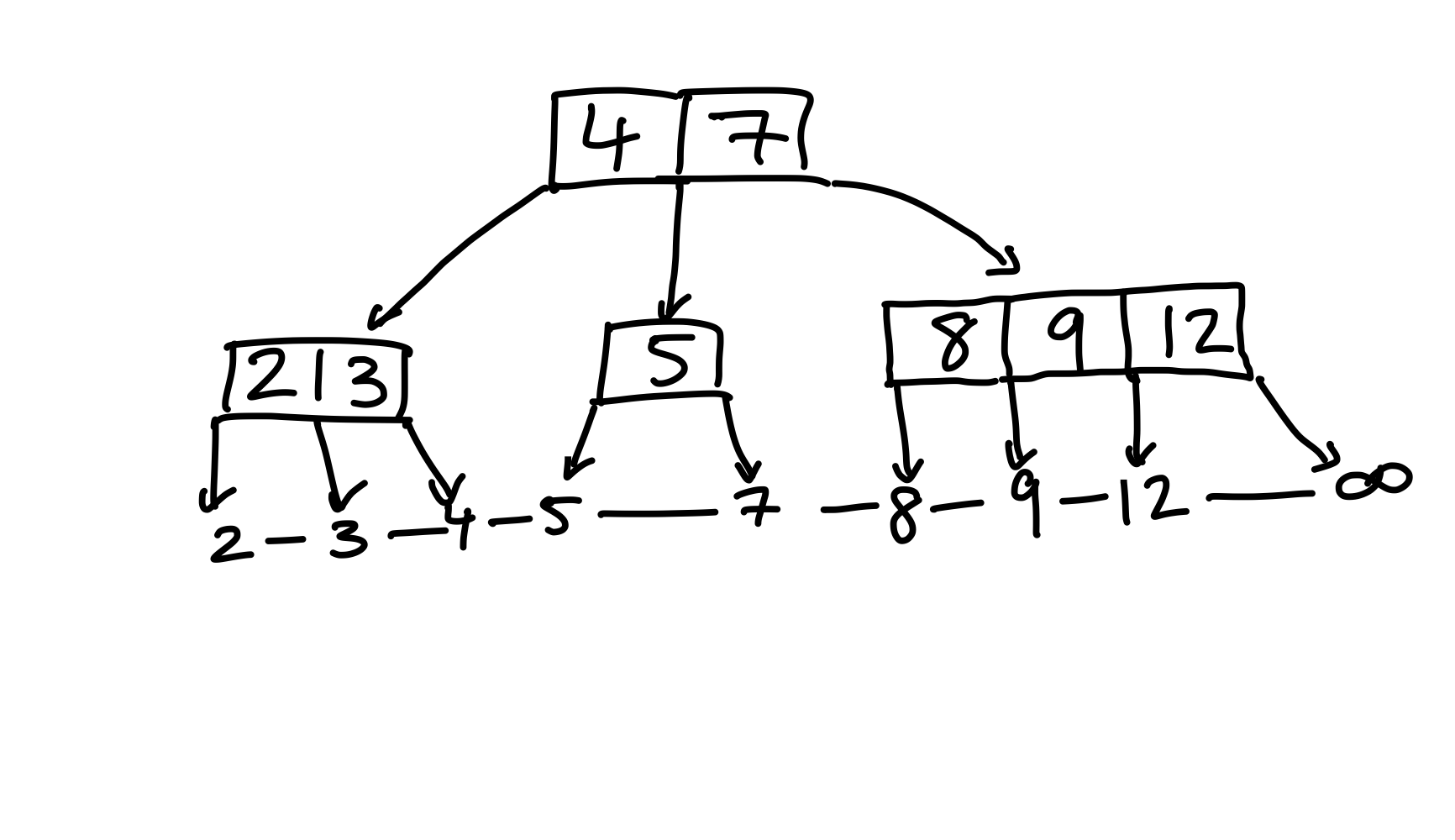
Figure 20: Nun löschen wir die 6 nicht bloß aus der verketteten Liste, sondern auch aus dem Baum.
Der Elternknoten hat jetzt zwei Kinder, das sind zuwenige, weshalb die (3, 5)-Bedingung wiederhergestellt werden muss. Dafür probieren wir, Schlüssel aus dem Geschwisterknoten umzuhängen, da dieser selbst nachdem ein Schlüssel abgegeben wurde noch genügend Kinder besitzt. Allerdings können wir nicht bloß einen Schlüssel umhängen, sonst wird die Ordnung des Baumes verletzt. Um das zu sehen, hängen wir einmal die \(8\) um.
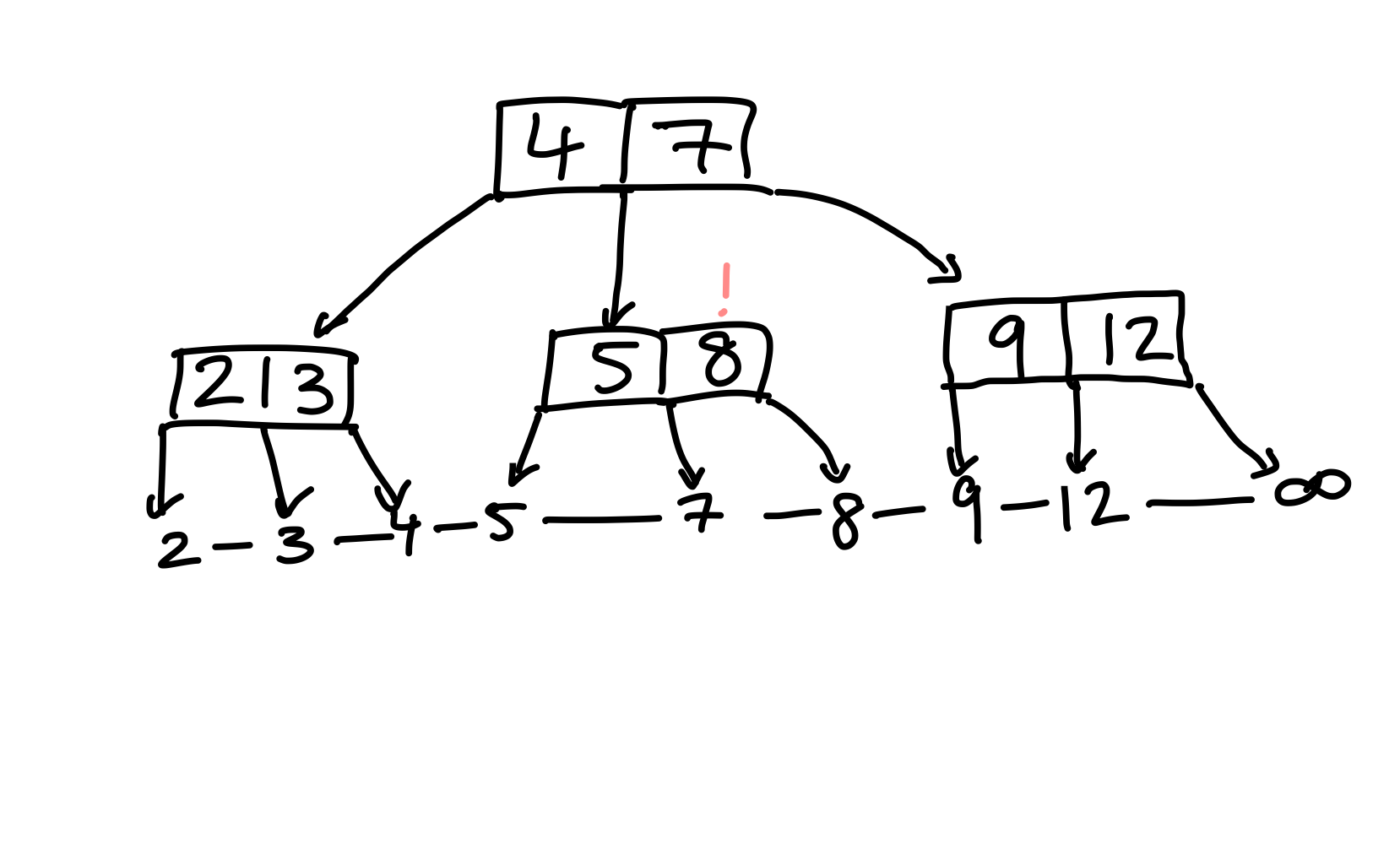
Figure 21: Schlüssel von Geschwistern einfach umzuhängen verletzt die Ordnung innerhalb des Baumes.
Suche ich nun nach der \(8\), so sagt die Wurzel mir, dass ich zum rechten Kind gehen muss. Dort finde ich die \(8\) aber nicht, sondern im mittleren Kind. Die Schlüssel im Elternknoten sind keine validen Schranken für die Schlüssel in Teilbäumen. Das ist schlecht. Um das Problem zu lösen, hängen wir in diesem Beispiel die \(7\), aus dem Elternknoten, mit um.
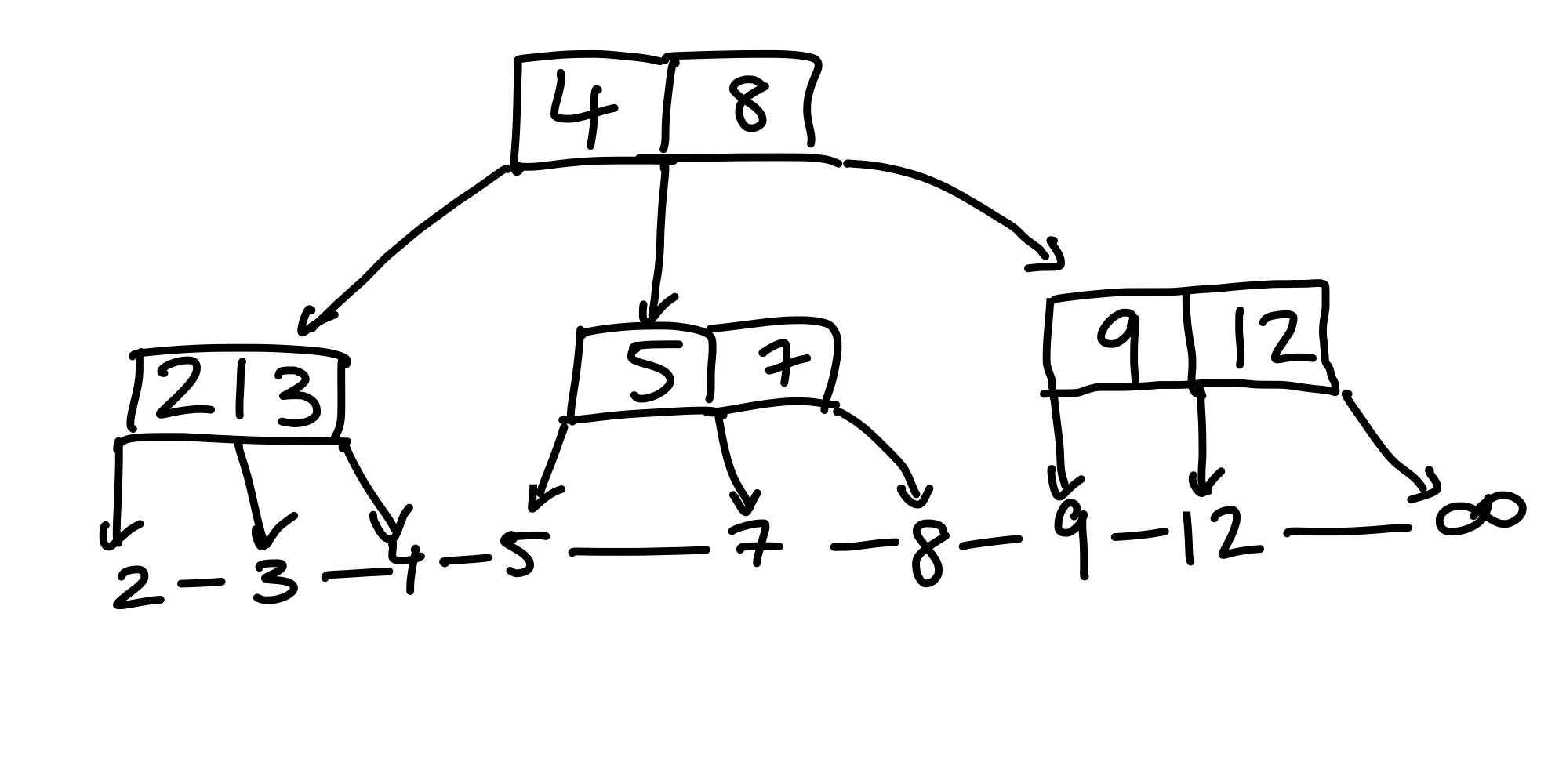
Figure 22: Berücksichtigen wir den verbinden Schlüssel, der im Elternknoten sitzt, wenn wir umhängen, so erhalten wir einen validen Baum.
Nun löschen wir die \(9\), und schauen was passiert.
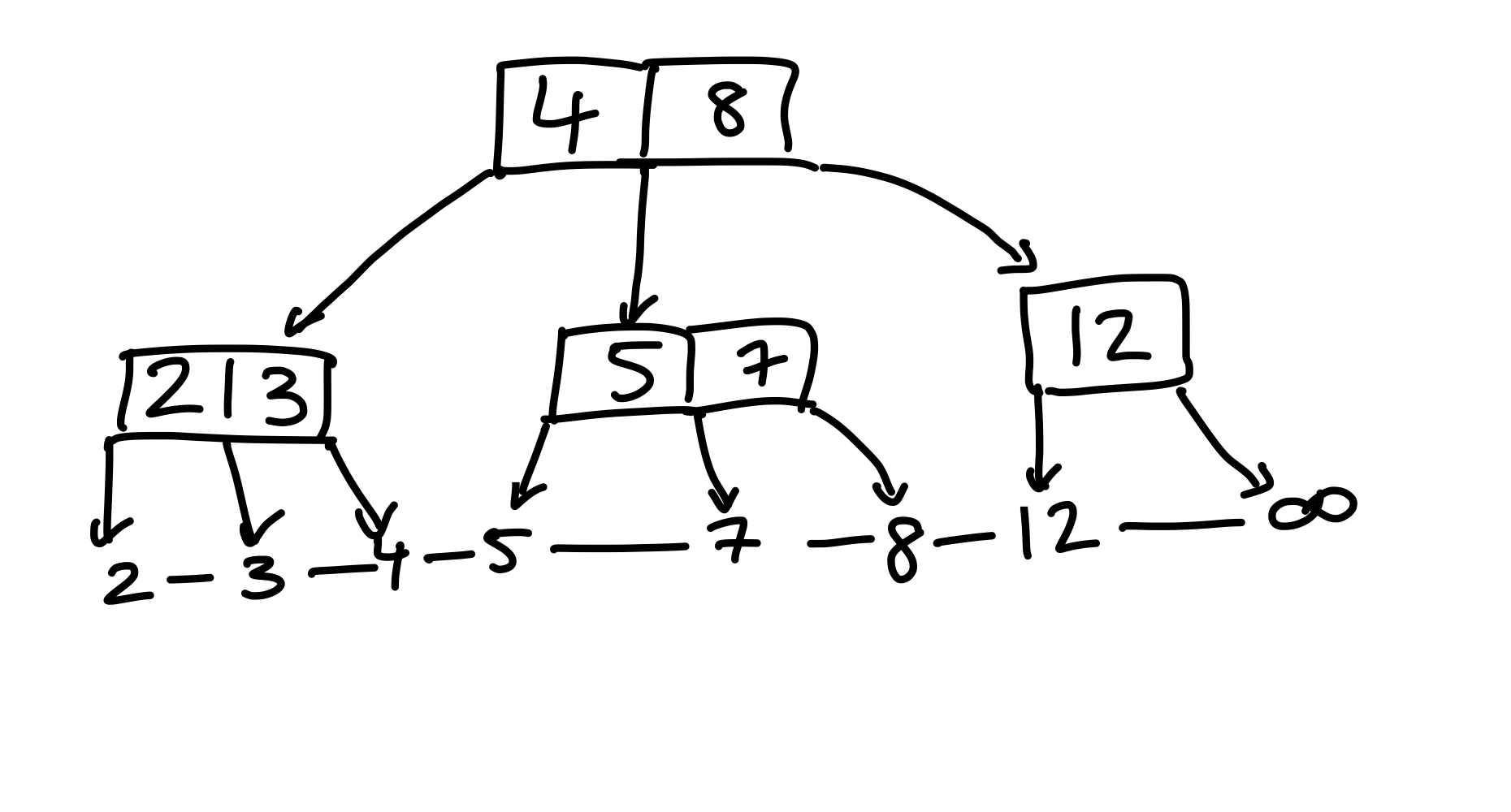
Figure 23: Das rechte Kind hat zu wenig Kinder, allerdings können wir keine Schlüssel umhängen, da sein linker Geschwisterknoten keine Schlüssel “übrig” hat.
Wieder hat ein Knoten zu wenig Kinder, allerdings können wir diesmal keine Schlüssel umhängen; schließlich besitzt der Geschwisterknoten selbst nur zwei Schlüssel. Sobald wir umhängen, verletzt er die (3, 5)-Bedingung. Stattdessen nehmen wir einen Schlüssel aus dem Elternknoten, und fügen ihn in unseren Knoten ein.
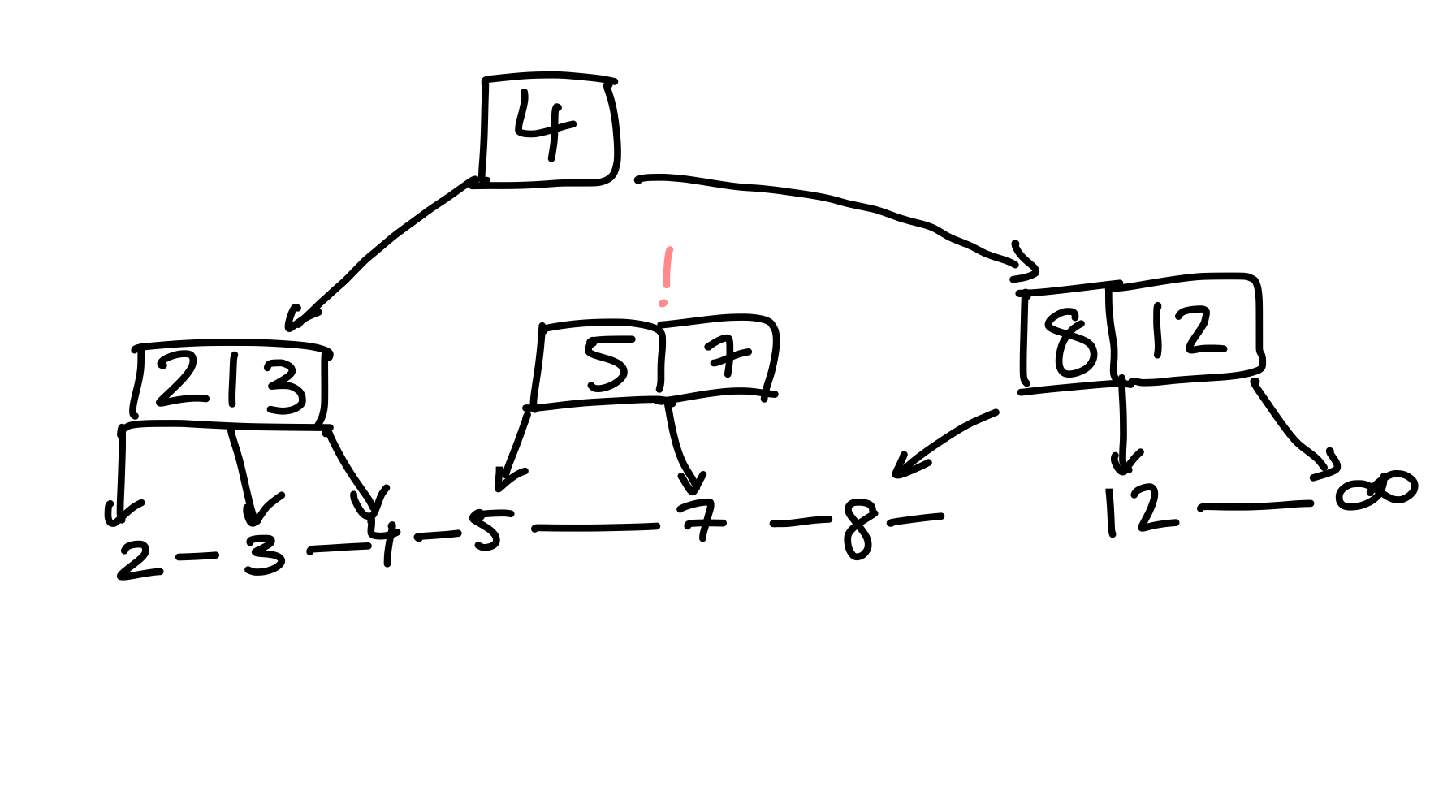
Figure 24: Nach Übertragen der 8 vom Elternknoten, verweist kein Zeiger auf das mittlere Kind.
Obwohl der Knoten die (a, b)-Bedingung erfüllt, haben wir ein Problem mit der Wurzel, diese hinterlässt ein Waisenkind – das mittlere Kind. Deshalb verschmelzen wir den Waisen mit unserem Knoten, wodurch wir einen validen (3, 5)-Baum erhalten.
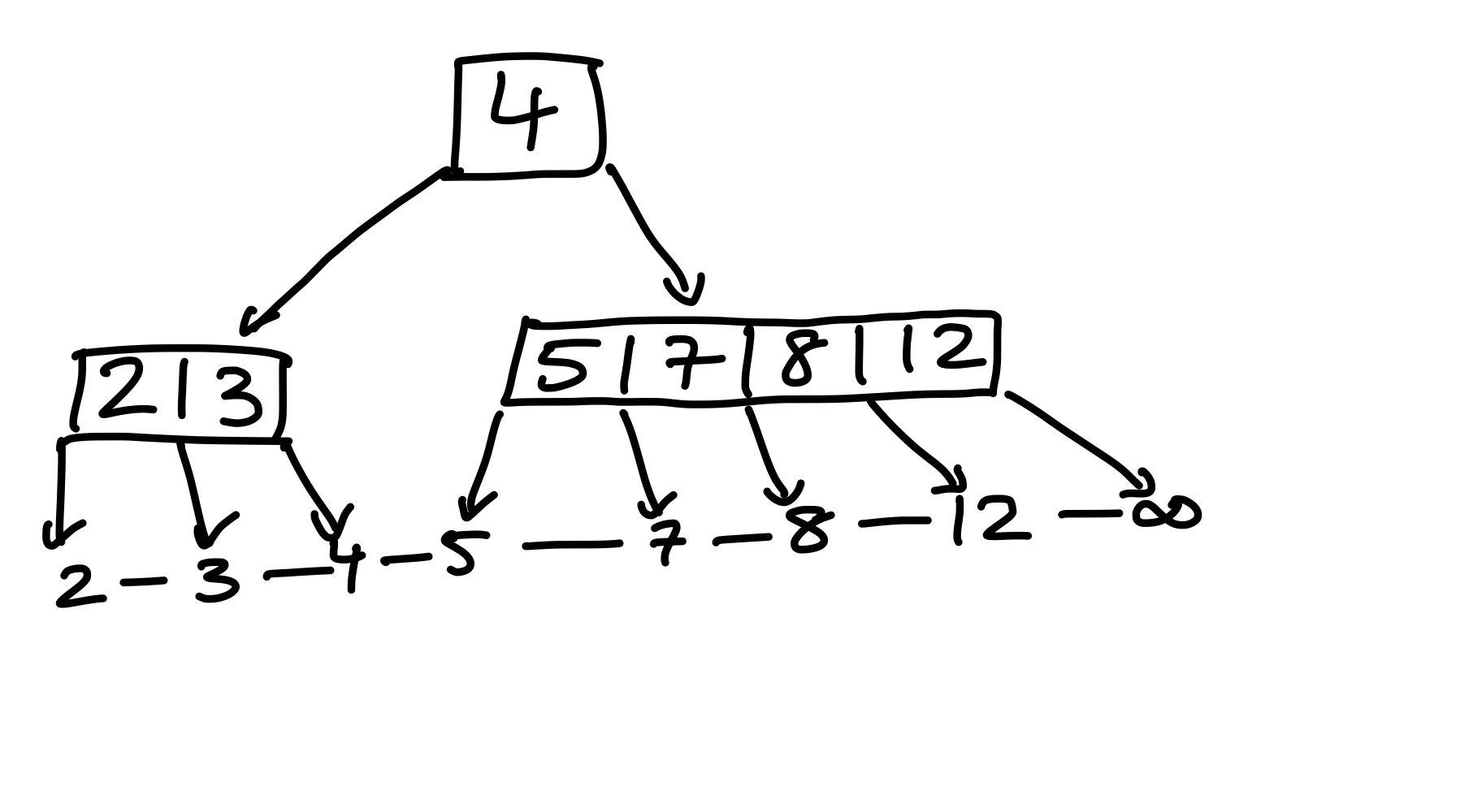
Figure 25: Den linken Geschwisterknoten zusätzlich zu verschmelzen liefert einen validen Baum.
Somit haben wir zwei Möglichkeiten für delete Operationen. Entweder, wir können Schlüssel von den Geschwistern umhängen – das nennt man rebalancieren – oder, wir müssen zwei Geschwister verschmelzen. Beim Letzteren nehmen wir noch einen zusätzlichen Schlüssel aus dem Elternknoten, damit die Ordnung im Baum gewährleistet ist.