Hashing
Unsere Reise durch die Algorithmik beginnt in der Regel mit Listen, für deren Operationen man eine \(\mathcal{O}(n)\) worst-case Laufzeit beweist. Mit dem Verlangen die Operationen zu beschleunigen, betrachtet man Prioritätswarteschlangen, in Form von (a, b)-Bäumen, wodurch wir die Laufzeit auf \(\mathcal{O}(\log n)\) reduzieren. Was aber, wenn wir in einer Echtzeit-A nwendung \(\mathcal{O} (1)\) Laufzeit benötigen? Können wir das geschickt umsetzen? Ja, mittels Hashing.
Eine Märchenwelt
Wo fangen wir an, wenn wir konstante Laufzeit erzielen wollen? Mit Operationen, die konstante Laufzeit benötigen. In diesem Fall betrachten wir Arrays genauer. Sobald ich weiss, in welchem Index ein Element gespeichert ist, kann ich es in konstanter Zeit erhalten. Das ist wichtig, da andere Datenstrukturen diesen instant access nicht ermöglichen. So müssen wir in einer verketteten Liste, beispielsweise, schrittweise zum gewünschten Index gehen. Wenn wir in konstanter Zeit Zugriff zu jeder Speicherzelle in einem Array erhalten, können wir in diese auch einfügen oder löschen. Das klingt erstmal super, wäre da nicht ein Problem: Wir wissen nicht, im vorhinein, wo ein Element gespeichert ist.
Stellen wir uns dennoch vor wir besitzen solch ein Orakel, das uns für jedes Element seinen Platz im Array verrät. Dann können wir unseren ursprüngliches Traum, von Operationen in \(\mathcal{O} (1)\) Laufzeit, wie folgt erzielen: Wir speichern ein Array, mit einer Größe proportional zur Eingabemenge. Konkret erstellen wir für \(n\) Elemente ein Array der Größe \(n\). Nun können wir bei jeder Operation das Orakel nach der Position fragen, und das Element dort einfügen, löschen, etc – alles in konstanter Zeit. Insbesonders müssen wir das Array zu keinem Zeitpunkt erweitern, was lineare Laufzeit zur Folge hätte, da wir die Größe passend gewählt haben.
Hier ein Beispiel, um zu sehen, dass diese Orakel existieren. Wir haben die Zahlen $0, …, 99, sowie ein Array der Größe \(100\). Hier können wir das Element selbst mit seinem Index identifizieren, so wird \(8\) im Index \(8\) gespeichert (wichtig: Arrayindizierung beginnt bei null!). Auch wenn das ein langweiliges Beispiel ist, sehen wir: Solche Orakel können existieren.
Ein weiterer wichtiger Punkt: Der Array access ist immer in konstanter Zeit möglich, egal wie groß das Array ist. Sobald wir ein Orakel besitzen, implementieren wir insert, delete, etc. in konstanter Laufzeit.
Zurück in die Realität
Zuvor haben wir ein Orakel als gottgegeben angenommen; es existiert einfach. Das ist bereits ein Problem, da in unserer Welt Orakel nicht vom Himmel fallen. Ein anderes Detail haben wir in der Märchenwelt ebenfalls ignoriert: Speicherbedarf. So haben wir ein riesiges Array angelegt, um alle möglichen Werte speichern zu können. In echt ist das nicht möglich, möchte ich, beispielsweise, alle möglichen Immatrikulationsnummern nach diesem Schema speichern, benötige ich ein Array der Länge \(10^{12}\) – zumindest ist meine Immatrikulationsnummer zwölf Ziffern lang, deshalb nehmen wir an, dass alle Immatrikulationsnummern zwölf Ziffern lang sind. Das erfordert zu viel Speicher, weshalb wir ein kleineres Array anlegen. Dadurch entstehen aller Hand Komplikationen.
Unser Orakel soll jedem Element eine Speicherzelle zuordnen, allerdings haben wir weniger Speicherzellen, als Elemente. Dementsprechend kann es passieren, dass zwei Elemente auf die gleiche Speicherzelle abgebildet werden – die Elemente kollidieren. Das ist schlecht, allerdings unvermeidbar, wenn wir eine große Menge in eine kleinere Menge abbilden. Bevor wir dieses Problem lösen, schauen wir uns an, wie so ein Orakel aussehen kann, und, dass Kollisionen unvermeidbar sind.
Angenommen, wir wollen die \(10^{12}\) Matrikelnummern auf ein Array der Größe \(10^{6}\) abbilden. Dafür könnte ich die Elemente der Reihe nach indizieren – \(1\) erhält den Index \(1\), \(1045\) den Index \(1045\), usw. – sobald wir am Ende des Arrays angekommen sind, indizieren wir wieder von vorne. Hier würde \(10^{6} - 1\) am Ende des Arrays eingefügt werden, \(10^{6}\) allerdings zu Beginn des Arrays. Das können wir durch die Funktion \(h\) modellieren:
\[ h(x) = x \text{ mod } 10^{6} \]
Diese Hashfunktion ordnet jedem Element einen Arrayindex zu. Allerdings können Elemente kollidieren, beispielsweise haben \(1\) und \(10^{6} + 1\) den gleichen Hash, sprich, den gleichen Wert \(h(x)\).
Insgesamt haben wir \(10^{6}\) Speicherzellen, für \(10^{12}\) Elemente. Hier bedeutet das, jeder Speicherzelle werden im Schnitt \(10^{12} / 10^{6} = 10^{6}\) Elementen zugeordnet. Kollisionen sind für diese Hashfunktion also unvermeidbar. Deshalb müssen wir Möglichkeiten haben, mit Kollisionen umzugehen. Schließlich können wir die Elemente nicht einfach ersetzen.
Auf Kollisionskurs
Gegeben eine Hashfunktion \(h\) , sowie zwei Werte \(x, y\) mit \(h(x) = h(y)\), wollen wir mit dieser Kollision umgehen. Dafür gibt es zwei Methoden: Chaining und lineares sondieren. Beim ersten befördern wir Speicherzellen zu verketteten Listen. Sobald eine Kollision auftritt, fügen wir das neue Element in die Liste an. Lineares Sondieren fügt das Element einfach an der nächsten freien Stelle im Array ein.
Chaining geht mit Kollisionen um, indem in eine verkettete Liste an eine Speicherzelle angehangen wird. Dadurch erhalten wir direkt ein Problem: Die linked lists können extrem lang werden. Um das zusehen, fügen wir einmal die Werte \(\langle 0, 10^{6}, 2 \cdot 10^{6}, … , 5 \cdot 10^{6} \rangle\) mit der obigen Hashfunktion ein.
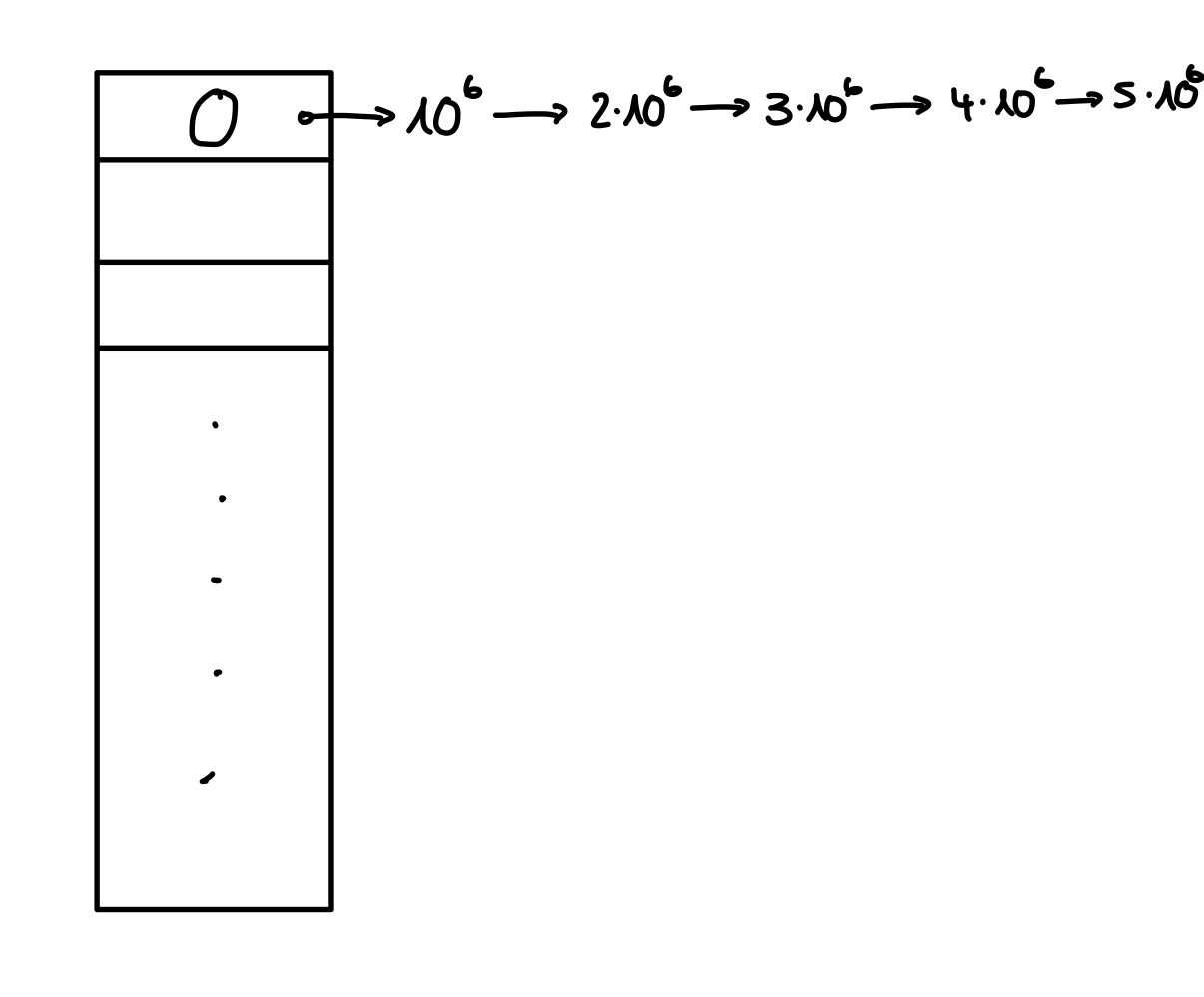
Figure 1: Chaining kann linked lists linearer Länge erzeugen.a
Das Beispiel illustriert ein fundamentales Problem: Im schlimmsten Fall kann eine Operation zur linearen Suche entarten, weshalb wir keine \(\mathcal{O}(1)\) Laufzeit, sondern \(\mathcal{O}(n)\) Laufzeit erhalten. Im schlimmsten Fall sind inserts in (a, b)-Bäume schneller. Das ist nicht das, was wir wollen. Noch schlimmer, selbst das Löschen von Elementen kann $ \mathcal{O}(n)$ Zeit benötigen, da das letzt Element einer linked List zu entfernen ebenfalls $ \mathcal{O}(n)$ Laufzeit benötigt. Mit chaining haben wir im worst-case nichts gewonnen, vielleicht funktioniert es mit linearem Sondieren besser.
Was mache ich, wenn eine Schublade in meiner Kommode gefüllt ist? Ich nehme die nächste, die frei ist. Auf Arrays übertragen suchen wir nach der nächsten freien Speicherzelle – das ist lineares Sondieren. Behandeln wir die Kollisionen in unserem Beispiel nun einmal durch lineares Sondieren, dann erhalten wir den folgenden Zustand.
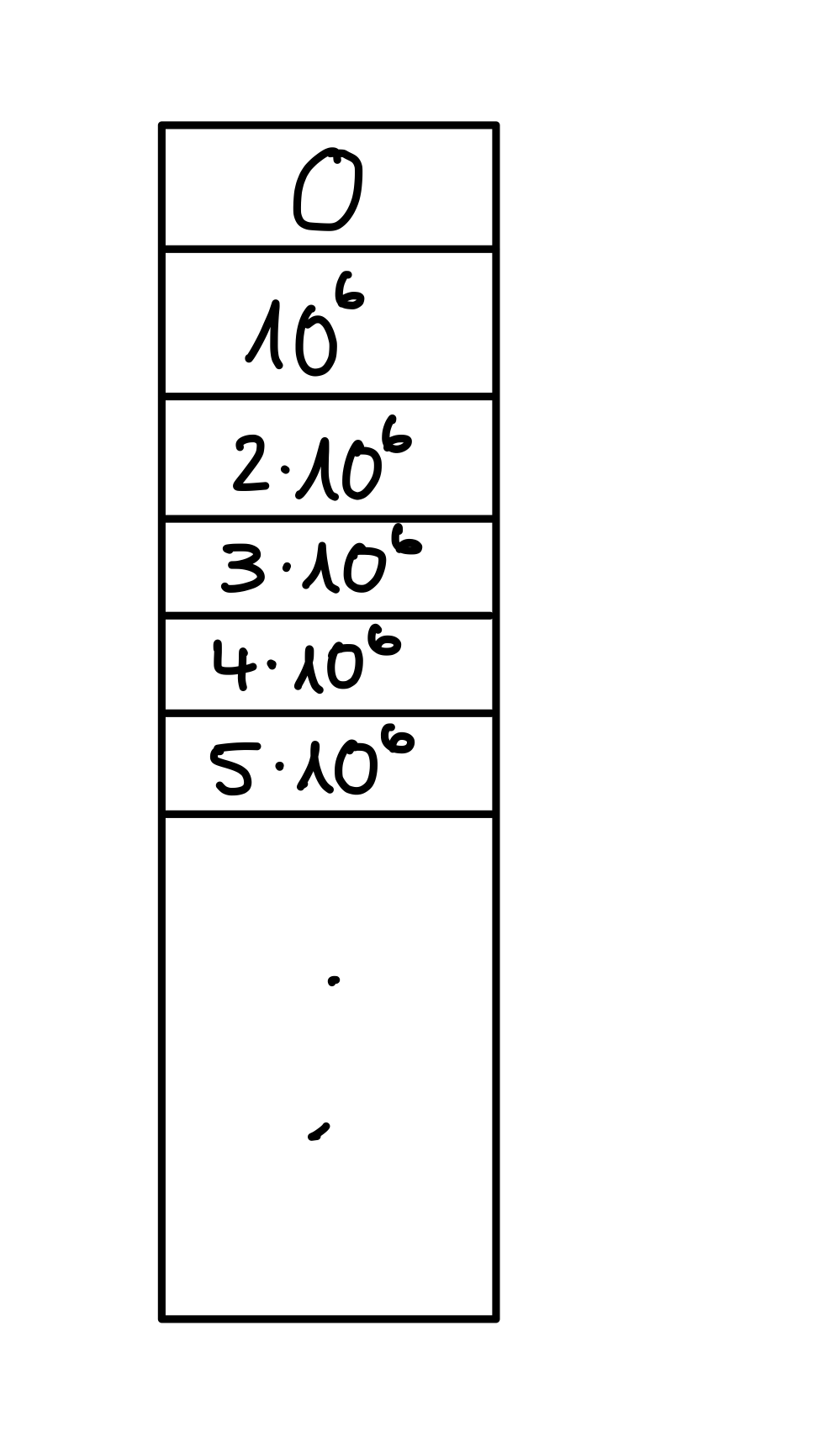
Figure 2: Lineares Sondieren kann länge Blöcke von Elementen, mit gleichem Hash erzeugen.
Eine Suche nach \(5 \cdot 10^{6}\) offenbart das gleiche Problem – es entartet zur linearen Suche. Wie beim chaining kann das Löschen ebenfalls zu linearer Laufzeit degenerieren, da wir das gesamte Array linear durchschreiten müssen. Das liegt daran, dass wir nach dem Löschen eines Elementes die entstehende Lücke schließen, indem nachfolgende Elemente aufgerückt werden, wenn diese denselben Hash haben. Löschen wir in unserem Beispiel \(2 \cdot 10^{6}\), müssen wir alle Folgenden Elemente nachrücken, was \(\mathcal{O}(n)\) viele sind.
Somit haben wir im worst-case keine konstante Laufzeit erzielt. Deshalb versuchen wir im folgenden Abschnitt, Hashfunktionen mit minimaler Kollisionswahrscheinlichkeit zukonstruieren.
Kollisionen vermeiden: Ein Schlichtungsversuch
Wenn die Bildmenge einer Abbildung kleiner ist, als der Definitionsbereich, dann existiert keine Funktion, welche auf einzigartige Elemente abbildet. Anders formuliert, kann eine Abbildung nicht injektiv sein, wenn der Definitionsbereich größer ist. Daraus folgt unmittelbar, dass sich Kollisionen für Hashfunktionen nicht vermeiden lassen. Allerdings können wir dennoch versuchen die Wahrscheinlichkeit einer Kollision zu minimieren.
Eine Funktion, welche die Wahrscheinlichkeit minimiert, sofern eine zusätzliche Bedingung gegeben ist, ist das Skalarprodukt. Zur Erinnerung: Gegeben zwei Vektoren \(x, y\) ist das Skalarprodukt definiert als \(\langle x, y \rangle = \sum_{i = 1} ^ n x_i y_i\). Jedoch nutzen wir für das Skalarprodukt zwei Vektoren, hashen aber im allgemeinen nur einen Vektor. Aus diesem Grund fixieren wir einen der Vektoren, um eine geeignete Hashfunktion zu erhalten. Wichtig ist, dass wir das Ergebnis des Skalarproduktes nochmal modulo einer Primzahl rechnen. Es ist kein Zufall, dass der Modulus prim sein muss, denn dann ist die Menge \(\mathbb{Z}_p\) ein Körper.
Nach diesen Anforderungen haben wir die folgende Menge an Hashfunktionen:
\[ H^{SP} := \{h_a : h(x) = \langle a, x \rangle \mod p\} \]
Um ein besseres Gefühl für diese Klasse an Hashfunktionen zu entwickeln, betrachten wir ein Beispiel. Schließlich ist noch garnicht klar, wie man Zahlen als Vektoren auffasst, usw.
Hashen mit dem Skalarprodukt
Sei nun \(p=13\) für unser Beispiel festgelegt, alle Rechnungen geschehen also modulo \(13\). Oder, anders betrachtet, hat unser Array genau \(13\) Speicherzellen. Zusätzlich bilden die 9-bit Strings unseren Definitionsbereich, das sind insgesamt \(2^{9}=512\) Stück. Jetzt müssen wir die Bitstrings aber mit unserem Modulus vereinen. Dafür unterteilen wir die Binärstrings in kleinere Stücke, welche mit \(p\) verträglich sind, indem wir berechnen, wieviele Bits nötig sind, um alle Zahlen innerhalb \(0, …, p - 1\) darzustellen. Das sind genau \(\lfloor \log(p) \rfloor = 3\) Bits. Daher teilen wir einen Bitstring der Länge \(9\) in drei Bitstrings der Länge drei auf. Somit wird \(x = 111010000_2\) in \(111\), \(010\) und \(000\) aufgeteilt. Diese interpretieren wir nun als natürliche Zahlen, modulo \(p\).
\[ 111_2 \equiv 7_{10} \\ 010_2 \equiv 2_{10} \\ 000_2 \equiv 0_{10} \]
Alles was fehlt, um einen Hash für \(x=111010000_2\) zu berechnen, ist ein \(a\). Da alle Inputstrings \(x\) in drei Bitstrings der Länge drei unterteilt werden, muss ein \(a\) ebenfalls aus drei Zahlen in \(\mathbb{Z}_p\) bestehen. In der Regel wählen wir die einzelnen Komponenten uniform zufällig. Für unser Beispiel sei \(a = (4, 10, 12)\). Jetzt haben wir bereits alles, um \(h_a(x)\) zuberechnen.
\[ h_a(x) = \langle a, x \rangle = 4 \cdot 7 + 10 \cdot 2 + 12 \cdot 0 = 28 + 20 + 0 \equiv 9 \mod 13 \]
So kann man mit dem Skalarprodukt einen Hash berechnen. Falls die Eingabe kein Bitstring ist, so müssen wir die Zahl erst als solche interpretieren. Beispielsweise würde \(x=464_{10}\) als \(111010000_2\) interpretiert werden.
Hashing mittels des Skalarproduktes ist nützlich, da es die Wahrscheinlichkeit einer Kollision sehr gering hält. Dazu folgender Satz:
Wenn \(h_a\) uniform zufällig aus \(H^{SP}\) gewählt wird, dann ist für \(x \neq y\) : \[ \Pr[h_a(x) = h_a(y)] \leq \frac{1}{p} \]
Für uns bedeutet das Folgendes: wenn wir \(a\) uniform zufällig wählen, und anschließend durch \(h_a\) hashen, dann erhalten wir eine geringe Kollisionswahrscheinlichkeit. Das ist gut, allerdings wollen wir $ \mathcal{O}(1)$ Laufzeit haben. Erzielen wir diese mit solchen Hashfunktionen? Im worst-case immernoch nicht, da, auch wenn die Kollisionswahrscheinlichkeit gering ist, es passieren kann, dass wir viele Kollisionen haben, weshalb die Operationen zu $ \mathcal{O} (n)$ degenerieren.
Allerdings können wir unter einer Annahme konstante erwartete Laufzeit erhalten. Dafür brauchen wir folgenden Satz:
Wenn \(n\) Einträge in ein Array der Größe \(p\) gehasht werden, dann erzielen alle Operationen eine erwartete Laufzeit von $ \mathcal{O}(1 + \frac{n}{p})$.
Wenn wir nun ein großes Array nutzen, können die Operationen in konstanter erwarteter Laufzeit implementiert werden. Dafür muss \(p = \Theta(n)\); wir benötigen also eine Speichermenge, die proportional zur Menge an Elementen wächst. Das stimmt mit der Intuition überein, die wir im Abschnitt Eine Märchenwelt hatten.
Konstante Zeit, Selbst im Schlimmsten Fall
Um selbst im schlimmsten Fall eine konstante Laufzeit zu garantieren, müssen wir Kollisionen komplett vermeiden; das steht im Widerspruch zu der Annahme, dass wir beim Hashing aus einer größeren, in eine kleinere Menge abbilden. Allerdings ist dies in manchen Fällen möglich, da wir nicht alle Schlüssel aus dem Definitionsbereich wirklich benutzen. Das Beispiel hier hat zwar die Möglichkeit einer Kollision, wenn wir alle möglichen Schlüssel betrachten, dennoch kann es Sequenzen geben, die wir ohne Kollisionen einfügen können. Das liefert uns Handlungsspielräume, da wir nicht über alle möglichen Schlüssel, sondern über eine konkrete Sequenz sprechen. In diesem Fall können wir Kollisionen vermeiden und erhalten einen perfekten Hash.
Sei \(\langle 3, 7, 2, 12, 30 \rangle\) gegeben, dann ist \(h(x) = x \mod 11\) eine perfekte Hashfunktion, für diese Sequenz, da wir die Hashes \(\langle 3, 7, 2, 1, 8 \rangle\) erhalten und diese voneinander unterschiedlich sind.
Insbesonders kann man durch uniformes Sampling relativ schnell eine perfekte Hashfunktion finden. Um das zu sehen hilft folgender Satz:
Für alle \(h \in H^{SP}\) ist \(\mathbb{E}[Kollisionen] \leq \frac{n(n-1)}{m}\).
Insbesonders hat die Hälfte der \(h \in H^{SP}\) weniger als \(2 \frac{n(n-1)}{m}\) Kollisionen.
Wenn wir \(m\) geschickt wählen, folgt daraus, dass die Hälfte dieser Funktionen weniger als eine Kollision hat – sie sind perfekte Hashes. Sobald \(m \geq n(n-1)\) ist das der Fall. Dementsprechend ist die Hälft der Funktionen ein perfekter Hash, wenn wir quadratischen Speicherplatz benutzen. Eine Schlussfolgerung: wir müssen im Durchschnitt bloß zwei solche Funktionen samplen, bis wir einen perfekten Hash erhalten.
c-Universelle Hashfunktionen
Zuvor haben wir gesehen, dass die Kollisionswahrscheinlichkeit beim Skalarprodukt relativ gering ist. Dafür gibt es einen Begriff, so ist \(H^{SP}\) eine 1-universelle Hashfunktion. Damit das Sinn ergibt, ist hier die Definition von c-universellen Funktionsfamilien:
Eine Funktionenfamilie1 \(H\) ist c-universell, wenn für \(x \neq y\) gilt, dass
\(\Pr[h(x) = h(y)] \leq \frac{c}{p}\), falls \(h\) aus \(H\) zufällig gewählt wird.
Das \(c\) gibt intuitiv an, wie wahrscheinlich Kollisionen sind. Für die Funktionenfamilie des Skalarproduktes haben wir gesehen, dass die Wahrscheinlichkeit durch \(\frac{1}{p}\) beschränkt ist. Unser \(c\) ist dort also eins. Je größer \(c\) wird, desto wahrscheinlicher werden Kollisionen, da die Schranke für die Wahrscheinlichkeit einer Kollision erhöht wird.
Eine häufige Frage ist: wie kann ich zeigen (oder widerlegen), dass eine Funktionenfamilie $c$-universell ist? Indem man die Wahrscheinlichkeit passend beschränkt, und zwar so, wie die Definition es vorgibt. Das kann frickelig werden, ist aber nicht unmöglich. Allerdings wird häufig gefordert, dass man die $c$-Universalität einer gegebenen Funktionenfamilie widerlegt. Da muss man nicht mehr Wahrscheinlichkeiten berechnen, sondern ein Gegenbeispiel finden. Konkret müssen wir zwei unterschiedliche Schlüssel \(x, y\) finden, für die es mehr Funktionen gibt, die kollidieren, als eine c-universelle Funktion das erlauben würde.
Konkretisieren wir das einmal. Gegeben seien die folgenden drei Funktionen, welche zusammen die Funktionenfamilie \(H\) bilden. Wir sollen nun widerlegen, dass \(H\) $2$-universell ist.
\[ h_0(x) = x \cdot 2 \mod 6 \\ h_1(x) = x \cdot 3 \mod 6 \\ h_2(x) = x \cdot 5 \mod 6 \]
Anders formuliert müssen wir zeigen, dass es ein Paar \(x,y\) gibt, sodass die Wahrscheinlichkeit einer Kollision bei zufällig gewähltem \(h\) größer als \(\frac{2}{6}\) ist.2 Bei uniform zufälligem samplen der Funktionen wählen wir jede mit Wahrscheinlichkeit \(\frac{1}{3}\). 3
Insgesamt setzt sich die kollektive Wahrscheinlichkeit einer Kollision zusammen aus der Summe der Wahrscheinlichkeiten, dass wir die Funktion \(h_i\) samplen – diese liegt bei \(\frac{1}{3}\) – und, dass die gesamplete Funktion eine Kollision induziert. Wir erhalten also folgende Formel für die Wahrscheinlichkeit einer Kollision:
\[ \frac{1}{3} \cdot (\Pr[h_0(x) = h_0(y)] + \Pr[h_1(x) = h_1(y)] + \Pr[h_2(x) = h_2(y)]) \]
Ob die Funktion für das konkrete Paar eine Kollision induziert hat entweder Wahrscheinlichkeit eins, oder null. Daher summieren wir in der Klammer lediglich auf, wieviele Funktionen eine Kollision erleiden. Somit können wir die Wahrscheinlichkeit auch wir folgt beschreiben:
\[ \frac{\text{Anzahl der Funktionen mit einer Kollision}}{3} \]
Um zu widerlegen, dass die Funktion $2$-universell ist, muss der obige Bruch größer als \(\frac{2}{6}\) sein.
\[ \frac{2}{6} < \frac{\text{Anzahl der Funktionen mit einer Kollision}}{3} \]
Wenn wir auf beiden Seiten mit drei multiplizieren, sehen wir, dass wir lediglich zeigen müssen, dass es eine ausreichende Anzahl an Funktionen gibt, welche eine Kollision bedingen.
\[ \frac{2 \cdot 3}{6} < \text{Anzahl der Funktionen mit einer Kollision} \]
Wenn zwei der Funktionen für ein von uns gegebenes Paar kollidieren, dann haben wir die $2$-Universalität bereits widerlegt. Ein solches Paar ist \((0, 6)\) – verifiziere gerne selbst, welche Funktionen hier kollidieren. Das liefert ein simples Kriterium zur Widerlegung von $c$-Univsersalität, wenn wir die Ungleichung generalisieren.
\[ \frac{c \cdot |H|}{p} < \text{Anzahl der Funktionen mit einer Kollision} \]
Hier müssen wir aufpassen, da die Anzahl der benötigten Kollisionen nicht bloß von \(c\) und \(p\) abhängt, sondern auch von der größe der Funktionenfamilie. Intuitiv kommt das daher, dass wir aus der Familie uniform zufällig wählen.
Wie Löscht Man Aus Einer Hashtabelle
Zusätzlich zu der insert-Operation gibt es die delete-Operation. Wie man ein Element löscht hängt davon ab, ob man chaining oder lineares Sondieren benutzt. Beim ersten löscht man das Element aus der verketteten Liste, beim Zweiten direkt aus dem Array. Beide Varianten haben einen ähnlichen Ablauf, zuerst suchen wir nach dem Element, falls es existiert löschen wir es, anschließend flicken wir die Lücke, die entstanden ist. Das sieht in beiden Varianten unterschiedlich aus, so müssen wir beim chaining sicherstellen, dass die verkettete Liste korrekt verbunden ist, wohingegen wir beim linearen Sondieren mehrere Optionen haben, mit den “Löchern” umzugehen.
Schauen wir uns zuerst an, wie man beim chaining ein Element löscht. Dafür betrachten wir das vorherige Beispiel, in dem wir eine einzige, lange linked List haben. Wenn wir \(3 \cdot 10^6\) löschen, fangen wir damit an den Hash zu berechnen4, darauffolgend sehen wir, dass der gesuchte Wert nicht in der gehashten Speicherzelle ist. Deshalb durchsuchen wir die linked list, bis wir den Wert finden. Anschließend löschen wir den Wert aus der linked list und freuen uns, da wir nichts mehr tun müssen und, weil das Löschen beim chaining relativ einfach ist.
:todo: Bild für delete mit chaining
Beim linearen Sondieren, allerdings, können wir auf mehrere Arten Werte löschen, entweder wir löschen die Werte und die Speicherzelle ist leer, oder wir markieren die Speicherzelle, um zu hinterlegen, dass hier zuvor gelöscht wurde. Anhand dieses Beispiels wenden wir einmal beide Varianten an. Dafür löschen wir wieder den Wert \(3 \cdot 10^6\). Wichtig ist, dass beide Varianten sich nur darin unterscheiden, was am Ende in der Speicherzelle liegt, nicht jedoch im Löschvorgang. Deshalb gehen beide gleich vor: es wird gehasht, in der Speicherzelle geschaut, ob das zulöschende Element vorhanden ist und falls nicht, wird das Array nach dem Wert durchsucht. In unserem Beispiel ist \(3 \cdot 10^6\) nicht in der gehashten Speicherzelle, daher betrachten wir die nächste 5. Diese enthält ebenfalls nicht den gesuchten Wert, weshalb wir wieder eine Speicherzelle weitergehen und tatsächlich fündig werden. Jetzt löschen wir den Wert aus dem Array. Beide Varianten sind hierunter veranschaulicht.
:TODO: Bild für delete mit beiden varianten
Allerdings bleibt eine viel wichtigere Frage: wozu brauchen wir beide Varianten überhaupt? Es klingt dumm, etwas als gelöscht zu markieren, wenn wir es auch einfach löschen könnten. Die zweite Variante erhält ihre Existenzberechtigung, wenn wir in einem Array mit “Löchern”6 einfügen wollen.
Dafür fügen wir in (:TODO: link example) \(5 \cdot 10^6\) ein – dieser Schlüssel existiert bereits in der Hashtabelle. Zuerst hashen wir und erhalten den Wert \(0\), weshalb wir mit dem Element in der ersten Speicherzelle vergleichen. Dieses entspricht nicht dem Einzufügenden; wir suchen also nach dem nächsten freien Platz. Das ist die dritte Speicherzelle im Array, in welche wir den Schlüssel einfügen.
Wo ist nun das Problem? Wir haben nun zweimal denselben Schlüssel in der Hashtabelle. Ein bereits existierender Schlüssel wurde beim traversieren nicht gefunden, weshalb wir diesen erneut eingefügt haben. Das ist schlecht. Wie sollen wir in Zukunft wissen, welches der beiden Elemente das Neuere ist? Außerdem kann es nach dieser Vorgehensweise passieren, dass wir mehr als zwei Kopien desselben Schlüssels speichern.7
Eine Lösung besteht darin, die entstehenden Lücken zu füllen, indem wir darauffolgende Elemente aufrücken. Allerdings müssen wir sicherstellen, dass wir ausschließlich Elemente aufrücken, die denselben Hash besitzen. Sonst kann es passieren, dass ein Schlüssel einem falschen Speicherplatz zugeordnet wird. Löschen wir nun aus unserem Beispiel den Schlüssel \(3 \cdot 10^6\) und füllen anschließend die entstehende Lücke. Dafür schauen wir in die darauffolgende Speicherzelle, und prüfen, ob der dort gespeicherte Wert denselben Hash hat. Das ist der Fall, weshalb wir den Schlüssel \(4 \cdot 10^6\) nach vorne rücken. Durch das Vorrücken entsteht wieder eine Lücke, die wir ähnlich füllen. Dazu prüfen wir, ob \(5 \cdot 10^6\) ebenfalls denselben Hash besitzt. Auch das ist der Fall, weshalb der Schlüssel auch vorrückt. Damit sind wir bereits am Ende angekommen, da die folgenden Speicherzellen leer sind.
:TODO: Bild, Schrittweises lücken füllen.
Wichtig: Es kann passieren, dass wir am Ende des Arrays ankommen. Dann können wir nicht einfach aufhören, sondern müssen für die erste Speicherzelle prüfen, ob diese denselben Hash besitzt, da es beim Einfügen passieren kann, dass wir in der letzten Speicherzelle eine Kollision haben, weshalb wir zum Beginn des Array gehen, um nach freien Speicherzellen zu suchen.
-
Funktionenfamilie bedeutet lediglich, dass wir eine Menge von Funktionen haben, aus der wir zufällig eine konkrete Funktion wählen. ↩︎
-
Wir teilen hier durch \(11\), da die Hashtabelle Größe \(11\) hat. Das können wir an dem Modulus der Funktionen sehen. ↩︎
-
Da wir \(3\) Funktionen haben. ↩︎
-
Das ist hier \(0\), da die Hashfunktion einfach modulo \(10^6\) rechnet. ↩︎
-
Wir gehen von der ersten Speicherzelle zur zweiten. Hier ist der Wert \(2 \cdot 10^6\) gespeichert. ↩︎
-
Hiermit meine ich Arrays, in denen mehrere Elemente, die denselben Hash haben, durch leere Speicherzellen getrennt sind. In dem Beispiel haben alle Schlüssel den gleichen Hash, allerdings sind diese nicht aufeinander folgend gespeichert. $ ⟨ 10^6, 2 ⋅ 10^6 ⟩$ und $ ⟨ 4 ⋅ 10^6, 5 ⋅ 10^6 ⟩$ haben den gleichen Hashwert, zwischen ihnen liegt allerdings eine leere Speicherzelle. ↩︎
-
Um zu sehen, dass ich keinen Stuss erzähle, kannst Du folgendes Beispiel berechnen. Auf dem Beispiel zum linearen Sondieren führst Du folgende Operationen aus: lösche \(4 \cdot 10^6\) und füge \(5 \cdot 10^6\) ein. Danach löschst Du \(3 \cdot 10^6\) und fügst dann \(5 \cdot 10^6\) ein, usw. Am Ende hast Du eine Hashtabelle, die viele Kopien von \(5 \cdot 10^6\) enthält. ↩︎